有界運算元
埃爾米特伴隨假設 H是一個希爾伯特空間，帶有內積。考慮連續線性運算元 A: H→ H（這與有界運算元相同）。
利用里斯表示定理，我們可以證明存在惟一的連續線性運算元
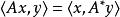埃爾米特伴隨
埃爾米特伴隨A*: H→ H具有如下性質：，對所有。
這個運算元 A* 是 A的伴隨。
這可以視為一個方塊矩陣的轉置共軛或伴隨矩陣推廣，在標準（復）內積下具有相似的性質。
性質
可得性質：
A** =A
如A可逆，則A* 也可逆，且 (A*)= (A)*
(A+B)* =A* +B*
(λA)* = λ*A*，這裡λ* 表示複數λ的復共軛
(AB)* =B*A*
1.A** =A
2.如A可逆，則A* 也可逆，且 (A*)= (A)*
3.(A+B)* =A* +B*
4.(λA)* = λ*A*，這裡λ* 表示複數λ的復共軛
5.(AB)* =B*A*
如果我們定義 A的運算元範數為
埃爾米特伴隨則
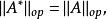埃爾米特伴隨而且有
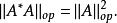埃爾米特伴隨希爾伯特空間 H上有界線性運算元與伴隨運算元以及運算元範數給出一個C*代數例子。
A的像與它的伴隨的核的關係為
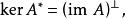埃爾米特伴隨
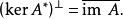埃爾米特伴隨埃爾米特運算元
有界運算元 A: H→ H稱為埃爾米特或自伴如果 A= A*這等價於
埃爾米特伴隨在某種意義下，這種運算元起著實數（等於他們的復共軛）的作用。他們在量子力學中作為實值可觀測量的模型。更多細節參見自伴運算元一文。
無界運算元的伴隨
許多重要的運算元不是連續的或只定義在希爾伯特的一個子空間上。在這種情形，我們仍然能定義伴隨，在自伴運算元一文有解釋。
其他伴隨
範疇論中，方程
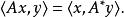埃爾米特伴隨形式上類似地定義了伴隨函子偶性質，這也是伴隨函子得名之由來。
參見
•數學概念
•線性代數
•內積
•希爾伯特空間
•埃爾米特運算元
•範數
•運算元範數
•線性映射的轉置
•物理套用
•對偶空間
•狄拉克符號
•量子力學
•可觀測量
