定義
在坡印亭的原始論文和許多教科書中，它通常記作 S或 N，定義為
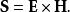能流密度矢量其中 E是電場強度； H是磁場強度。
這種形式通常被稱為 亞伯拉罕形式。偶爾也用電場強度 E和磁感應強度 B作為另一種定義。甚至可以把電位移矢量 D和磁感應強度 B結合起來得到的坡印亭矢量的 閔可夫斯基形式，或使用 D與 H構成另一種形式。選用哪種形式一直是有爭議的：羅伯特·費福（Robert Pfeifer）等人總結並一定程度上解決了亞伯拉罕與閔可夫斯基形式支持者之間長達一個世紀的爭議。
坡印亭矢量表示的是電磁能量的能流矢量的特殊情況。然而，空間內任何形式的能量都有其移動方向，也有密度，所以其他形式的能量也可以定義能流矢量，例如機械能。1874年由尼科萊·烏諾夫發現的烏諾夫–坡印亭矢量以完全廣義的觀點描述了液體和彈性介質中的能流。
微觀領域的形式
在某些情況下，可以更合適地定義坡印亭矢量為
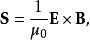能流密度矢量其中μ是真空磁導率； E是電場強度； B是磁感應強度。
可以直接從以總電荷和總電流為變數的麥克斯韋方程組和洛倫茲力定律導出這種形式。
對應的坡印亭定理的形式為
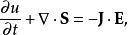能流密度矢量其中 J為 全電流密度，而能量密度 u為
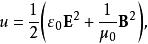能流密度矢量其中 ε是真空電容率。
坡印亭矢量的兩種定義在真空或非磁性材料中等價，其中 B= μ H。在其他的情形，兩者的差異在於 S= 1/μ E× B，而對應的 u是純輻射性的，因為耗散項− J⋅ E包括了總電流，而以 H場所做的定義涵蓋了約束電流的貢獻，因而缺乏耗散項。
推導 S= 1/μ E× B的過程中只需要微觀場 E和 B，關於材料性質的假設則可迴避掉。是故以此方式定義的坡印亭矢量與坡印亭定理是普遍成立的，不論是在真空中或各式各樣的材料中。
例子與套用
同軸電纜
舉例而言，一條同軸電纜的介電絕緣體之中的坡印亭矢量與電纜的軸線幾乎平行（假設電纜外無場，且包含直流電在內的波長遠長於電纜直徑）。輸送到負載的電能完全是流經導體之間的介電質。極少量的能量是經導體流動，因為此處的電場強度接近於零。在導體內的能量流是徑向的，成為導體電阻發熱的能量散失。無能量流至電纜外，因為內層導體與外層導體所產生的磁場彼此相抵消。
電阻耗散
若導體有不小的電阻，則在導體表面附近，坡印亭矢量則會出現歪斜而接觸到導體。當坡印亭矢量伸入導體時，其被彎折到幾乎與表面垂直的方向。此為斯涅爾定律以及導體內部甚慢的光速所造成的結果。
在導體內部，坡印亭矢量代表了能量從電磁場流入電纜，產生了電阻的焦耳發熱。
靜場
在靜態場考慮坡印亭矢量顯示出了麥克斯韋方程組的相對論性，並讓我們更加理解了洛倫茲力 q( v× B)的磁分量。例如，考慮所附圖片，它描述了在一個圓柱形電容器的坡印亭矢量，位於在由永磁體產生的一個磁場（指向紙內）。雖然只有靜態電場和磁場，計算坡印亭矢量得出了順時針方向循環流動的沒有起始或結束的電磁能量。
雖然循環的能流看似是無意義或矛盾的，它卻證明了保持動量守恆是絕對有必要的。動量密度與能流密度成正比，所以能量的循環流動包含著 角動量。這是因為洛倫茲力的磁分量存在時，電容器放電。在放電過程中，能流中包含的角動量隨著轉移到穿過磁場的放電電流的電荷上而耗盡。
