 地平線
地平線簡介
 地平線
地平線在很多情況下,特別是在透視圖里,地面的曲率傳統上被忽略,而地平線則被當為地面和畫面的交線。值得注意的是,當觀看者接近地面時,幾何地平線(假設地面為平的、無限廣闊的)與真地平線(即地面為曲面)的差距變得很少。所以即使地面真的是平的,仍會存在一條可見地平線,而對站在真正平的地面的觀看者來說,其看到的地平線的位置與外表與站在曲的地面的觀看者所看到的差距並不大。
在天文學裡,地平線指觀看者所看到的地平面。其為地平座標系的基本平面,而在其上的點的軌道有著零度的地平緯度。就如上述的幾何地平線般,在天文學裡的地平線可以被當作太空里的平面,而非畫面上的線。
據典故記載,在中國古代,人們常把地平線稱作天涯。
計算
 海天交接處,古人稱之“天涯”
海天交接處,古人稱之“天涯”站在平原上、高塔上或被平原包圍的山丘上時,與地平線的距離大約為
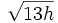 (圖)地平線
(圖)地平線例子:
則在平面上,h = 1.70米,則與地平線相距4.7公里
站在山丘或高塔上,高度為100米,與地平線相距36公里
這些數字指出人們在地平面上的理論能見度(當然亦會因空氣的清晰度而改變)。當計算與高塔尖的距離時,因為船的桅桿或山丘在地平線上,所以需要加上其高度所產生的水平距離。如站在地面時,h = 1.70米,若天氣許可的話,人們則可以在距高塔41公里的地方清楚看到高100米的高塔塔頂。
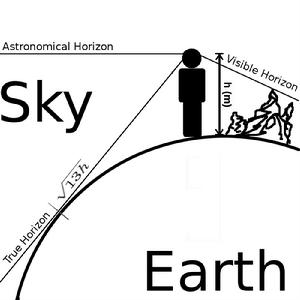 三種地平線
三種地平線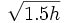 (圖)地平線
(圖)地平線當h少於地球半徑時(6371公里),公制的公式是合理的(英制的公式亦頗精確)。而即使在人造衛星上亦適用的準確的計算由觀看點與地平線的距離公式為
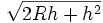 (圖)地平線
(圖)地平線另一條公式為:
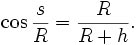 (圖)地平線
(圖)地平線這公式可計算地面與觀看者所處地的底部(如塔底)的曲線長度距離s,反之,上一個公式則是觀看者眼睛與地平線的直線視距。兩道公式均假設了觀看者高度相對地球半徑來說可以被忽略。
![地平線[詞語解釋] 地平線[詞語解釋]](/img/1/c4a/nBnauM3X0MDMxkTNwkzMzkDMwQTM2QjN5ETNyQTNwAzMwIzL5MzLxQzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg)
