簡介
圓環坐標系(英語:Toroidal coordinates)是一種三維正交坐標系。設定二維橢圓坐標系包含於 xz-平面;兩個焦點F與F的直角坐標分別為 (-a, 0, 0)}與(a,\0, 0)}。將雙極坐標系繞著 z-軸旋轉,則可以得到圓環坐標系。雙極坐標系的兩個焦點,變為一個半徑為 a 的圓圈,包含於圓環坐標系的 xy-平面。稱這圓圈為 焦圓,又稱為 參考圓。
數學定義
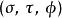 圓環坐標系
圓環坐標系在三維空間裡,一個點 P 的圓環坐標最常見的定義是
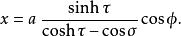 圓環坐標系
圓環坐標系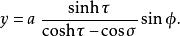 圓環坐標系
圓環坐標系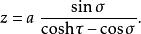 圓環坐標系
圓環坐標系 圓環坐標系
圓環坐標系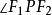 圓環坐標系
圓環坐標系 圓環坐標系
圓環坐標系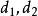 圓環坐標系
圓環坐標系其中, (x,\y, z) 是直角坐標, 坐標是的弧度, 坐標是點 P 離兩個焦點的距離的比例的自然對數:
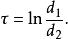 圓環坐標系
圓環坐標系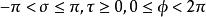 圓環坐標系
圓環坐標系圓環坐標的值域為。
坐標曲面
 圓環坐標系
圓環坐標系每一個-坐標曲面都是包含了焦圓,而不同心的圓球面。圓球半徑為
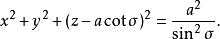 圓環坐標系
圓環坐標系 圓環坐標系
圓環坐標系 圓環坐標系
圓環坐標系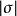 圓環坐標系
圓環坐標系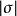 圓環坐標系
圓環坐標系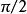 圓環坐標系
圓環坐標系正值 的圓球面的圓心都在正 z-軸;而負值的圓球面的圓心則在負 z-軸。當絕對值增加時,圓球半徑會減小,圓心會靠近原點。當圓心與原點同點時,達到最大值 。
 圓環坐標系
圓環坐標系每一個-坐標曲面都是不相交的環面。每一個環面都包圍著焦圓。環面半徑為
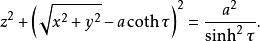 圓環坐標系
圓環坐標系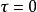 圓環坐標系
圓環坐標系 圓環坐標系
圓環坐標系曲線與 z-軸同軸。當 值增加時,圓球面的半徑會減少,圓球心會靠近焦點。
標度因子
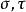 圓環坐標系
圓環坐標系圓環坐標的標度因子相等:
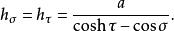 圓環坐標系
圓環坐標系方位角的標度因子為
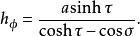 圓環坐標系
圓環坐標系無窮小體積元素是
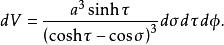 圓環坐標系
圓環坐標系拉普拉斯運算元是
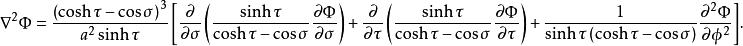 圓環坐標系
圓環坐標系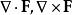 圓環坐標系
圓環坐標系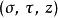 圓環坐標系
圓環坐標系其它微分運算元,像 ,都可以用坐標表示,只要將標度因子代入在正交坐標系條目內對應的一般公式。
套用
圓環坐標有一個經典的套用,這是在解析像拉普拉斯方程這類的偏微分方程式。在這些方程式里,圓環坐標允許分離變數法的使用。個典型的例題是,有一個圓環導體,請問其周圍的電位與電場為什麼?套用圓環坐標,我們可以精緻地分析這例題。
由於托卡馬克的圓環形狀,圓環坐標時常用在托卡馬克的核聚變理論研究。
