圓型限制性三體問題

簡介

研究一個無限小質量體在兩個有限質量體（圍繞公共質點作圓周運動）的萬有引力作用下運動的規律問題。在航天活動中，可以把太空飛行器看作一個無限小質量體。太空飛行器在地球-月球引力作用下，或者在太陽-地球引力作用下,或者在太陽-某大行星引力作用下的運動問題，都可以近似看地成圓型限制性三體問題。

能量積分

在研究圓型限制性三體問題時採用一個與兩個有限體一起運動的鏇轉坐標系。坐標原點在公共質心上，圖中標出了X、Y軸的方向,P1、P2為兩個有限質量體，X-Y平面是兩個有限質量體運動的平面。Z 軸與X、Y軸垂直。在這個參考坐標系中,無限小質量體的運動速度與位置有下面的關係：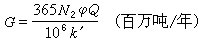
式中v為無限小質點在鏇轉坐標系中的速度；x、y、r1、r2分別為小質點的位置坐標和到P1、P2的距離；G為萬有引力常數；m1、m2分別為P1和P2的質量；C為積分常數，它依賴於無限小質點初始位置和初始速度。這個公式是圓型限制性三體問題的能量積分，常稱為雅可比積分。僅有這個關係式還不能描述小質量體的運動。迄今為止圓型限制性三體問題還沒有解出。無限小質量體的實際運動只能用數值計算方法求解。 太空飛行器在地球-月球引力作用下的運動，用能量積分不僅能夠給出太空飛行器的位置與速度的關係，並且從中可以引出零速度面和平動點兩個有用的概念。

零速度面

在能量積分的公式中,當V等於0時，公式描述了一個空間曲面，稱為零速度面。它是太空飛行器所能夠達到的範圍與不能達到的範圍的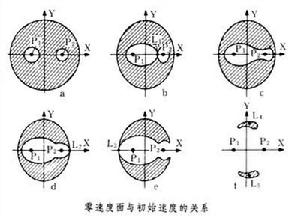

圓型限制性三體問題

分界面。零速度面與太空飛行器的初始位置和初始速度有關。在初始位置一定的情況下,初始速度增加，太空飛行器所能達到的範圍增大,不可到達的範圍縮小。圖中P1和P2分別代表地球和月球，陰影部分表示太空飛行器不能到達的區域，圖中a～f表示隨著初始速度增加不能到達的範圍縮小的過程。在a中,兩個卵形區域互不連通，這表明在這樣的初始速度下太空飛行器不可能到達月球。在b中兩個卵形區域相切於L1點,與它對應的速度是從地球發射太空飛行器可能到達月球的最小速度。在c中兩個卵形區相通,從地球發射的太空飛行器可能從裂開的視窗飛往月球。在d中零速度面相切於L2點,太空飛行器不能逃逸出地-月系統。有e中零速度面再次相切於L3點。在f中零速度面收縮到L4、L5兩點。距地面 200公里處的太空飛行器在初速為10.848公里/秒時，就會出現b的情況，這是飛向月球的最小速度。d 所對應的初速為10.849公里/秒,要想脫離地-月系統,太空飛行器的初速不得小於這個數值。e和f所對應的初速分別為10.857公里/秒和10.858公里/秒，在這幾種情況下的初速相差很小。

平動點

是指零速度面隨初始速度而變化的過程中新出現的零速度面的三個切點(圖中的 L1、L2、L3)和兩個消失點(圖中的L4、L5)。其中L1、L2和L3處在地－月連線上。L4(或L5)與地球和月球是等邊三角形的三個頂點。平動點是太空飛行器運動的特解。在鏇轉坐標系中如果在平動點上有初速為零的太空飛行器，則太空飛行器的速度將始終為零，也就是說，它在鏇轉坐標系中是不動的太空飛行器。實際上太空飛行器是圍繞地球作圓周運動，它的運動角速率和月球的相同。在平動點周圍運動的太空飛行器具有特殊的作用。（見暈軌道）。