月球探測器軌道運動
正文
月球探測器的質心運動。它有兩個特點：①在地球和月球之間運行時常常是在地球引力和月球引力共同作用下運動。這類運動問題可以近似地看成是圓型限制性三體問題。要接近月球，太空飛行器相對地球的初始速度不得小於 10.848公里/秒。②地球相對於太陽的作用球半徑為93萬公里（見行星探測器軌道）。月球與地球之間的距離只有38萬公里，月球探測器沒有脫離地球引力範圍，它的過渡軌道可以是相對地球的橢圓。發射探測器的初速不一定要超過逃逸速度(見太空飛行器軌道速度)。這兩個特點反映了月球探測器軌道與人造地球衛星運行軌道、行星探測器軌道的差異。月球探測器軌道運動按近似分析方法分為兩個階段：一個是以地球引力為主的階段；另一個是以月球引力為主的階段。兩者以月球相對於地球的作用球半徑為 6.6萬公里的球面為分界。當太空飛行器與月球的距離大於 6.6萬公里時，認為太空飛行器受到的力主要是地球引力，並近似地認為太空飛行器相對地球的軌道是克卜勒軌道。當太空飛行器進入月球作用球時,認為太空飛行器是相對於月球運動。如果將進入月球作用球的速度換算成相對月球的速度，這個速度往往超過月球的脫離速度，因而太空飛行器相對月球的軌道是雙曲線。兩個階段軌道連線起來就是月球探測器的軌道。這種近似方法稱為雙二體問題。如果兩個階段的軌道都用太空飛行器軌道攝動的方法解出，可以得到比較精確的軌道。月球探測器軌道依順序可以分為停泊軌道和過渡軌道,過渡軌道一直延伸到月球附近。此後,不作機動飛行時便分為擊中月球軌道和繞飛軌道；作機動飛行時，可成為月球衛星軌道或在月球表面軟著陸。對於需要返回地球的太空飛行器，太空飛行器還將進入返回軌道。在實際工作中，軌道計算以數值方法為主，以近似分析方法為輔助手段。軌道設計的主要任務是選擇過渡軌道和確定機動飛行的方案。
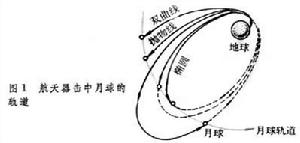
擊中月球軌道 簡單的定性分析方法是假設月球是一個沒有引力的幾何球體。用這一方法所得到的結果與雙二體分析方法的結果相差不大。選擇適當的發射時間，使月球與太空飛行器的軌道相交，太空飛行器就能擊中月球。太空飛行器擊中月球的軌道可以是直線、橢圓、拋物線或雙曲線。對於橢圓軌道有三種相交的方式：過了遠地點後相交（下降型）；在到達遠地點前相交（上升型）和在遠地點處相交（相切）。只有下降型才可能擊中月球背面（圖1）。實際上,太空飛行器在飛往月球的過程中還受到太陽的引力和月球的引力，因此，實際運行路線更複雜一些。為了擊中月球，太空飛行器對於初始速度的大小和方向都有較高的要求（速度誤差為幾十米每秒，方向為零點幾度）。發射時間與月球所在的位置和月球的運動有關，也需要嚴格控制。如果還要太空飛行器擊中月球表面的特定區域，則精度的要求更高。在太空飛行器飛向月球的途中往往需要修正軌道。
月球探測器軌道運動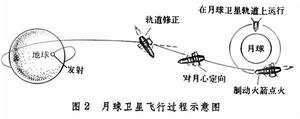
月球探測器軌道運動月球著陸軌道 探測器可以從接近月球的軌道上直接著陸於月球，也可以從月球衛星軌道上經過機動飛行在月球上著陸。但無論哪一種著陸方式，由於月球沒有大氣層，都需要在探測器下降過程中用火箭發動機制動，以使探測器實現在月球上軟著陸（見月球著陸）。
飛越月球軌道 探測器繞過月球飛行的軌道。當探測器進入月球作用球邊界時，探測器相對月球的速度是雙曲線軌道速度，並相對月球作雙曲線運動。飛出月球作用球時的速度和進入作用球時的速度大小相同，方向轉過一個角度。這時探測器相對地球的速度大小和方向都發生了變化。飛越的效果使得探測器加速或者減速。加速的結果可能使探測器獲得脫離地球的逃逸速度，這樣探測器離開地球時速度雖然小於第二宇宙速度，但是藉助月球引力仍能成為人造行星。有人構想，發射地球靜止衛星時也採用飛越月球的過渡軌道，軌道平面由月球引力扭轉到地球赤道平面內，並且過渡軌道的近地點正好是同步軌道半長軸，在近地點減速後衛星就會成為地球靜止衛星。用這樣的方式發射地球靜止衛星，只有當月球位於地球赤道平面內時才有可能。這種機會一個月可以遇到兩次，發射場緯度比較高時採用這種方式比一般的方式能節省能量（見靜止衛星發射和定點）。
