圓內角

如圖，在⊙O中，弦AB、CD交點P。則弦AB、CD所成的4個角便是⊙O的圓內角，即∠APC、∠CPB、∠BPD和∠APD是⊙O的圓內角。

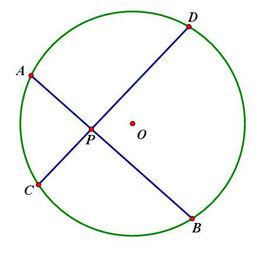
定義

圓的兩條弦在圓內相交所成的角叫做圓內角。

性質

圓內角定理

圓內角的度數等於這個角（及其對頂角）所對的弧的度數之和的一半。

圓內角定理的推導過程

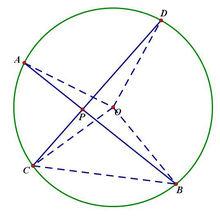圓內角定理的推導

如右圖，已知在⊙O中，弦AB、CD交於點P。

連OA、OB、OC、OD和BC。

圓內角

在⊙O中，∠BCD= ∠BOD（圓周角定理）；

圓內角

同理，∠ABC= ∠AOC。

∵∠APC是△PCB的外角，

∴∠APC=∠BCD+∠ABC

圓內角

圓內角

= ∠BOD+ ∠AOC

圓內角

= (∠BOD+∠AOC)

∴圓內角的度數等於這個角（及其對頂角）所對的弧的度數之和的一半。