定義
四線擺平台可繞中心軸線作扭轉擺動，若將平台沿某一方向拉離平衡位置後放開，平台擺動的軌跡將通過畫筆記錄在這張紙上，稱為四線擺曲線。
特性
四線擺曲線的多層次結構反映了在阻力的作用下平台擺幅逐漸減小，因此曲線不可能重合。四線擺曲線的形狀隨平台的擺動狀態而變，平行擺動為直線，圓周擺動為螺旋線，扭動擺動則會畫出豐富多彩的曲線，而且沒有任何兩次扭擺畫出的曲線相同。
生成方法
用四條直線吊住一個平板,使其能在水平面內做任意方向的擺動，在上面鋪一張白紙，然後用一個固定的臂來固定一支筆，使筆不會因為平板的擺動而運動，但筆尖要接觸白紙,準備好後，任意晃動平板，可以看到白紙上留下的軌跡就是四線擺曲線。
下兩圖所示即為兩次不同的四線擺曲線，與上述記錄方法不同，不是用筆在紙上描繪出的曲線，而是用安放在四線擺平台上的點光源隨四線擺運動時在照相機鏡頭前長時間曝光所留下的光跡。
四線擺曲線(光跡)
四線擺曲線(光跡)四線擺的平動
把平台的擺動分解在兩互相垂直的方向上（設為 x 軸和 y 軸），平台的小角度扭轉擺動可看作簡諧運動，若它們的頻率相同，振動表達式分別為
x=A1cos( ω t+ ф 1 )
y=A2cos(ωt+ф2)
消去參數 t ，即可得質點的軌跡方程為
x/A1+y/A2 -(2xy/A1A2)cos( ф 2 - ф 1 )=sin( ф 2 - ф 1 )
一般的說，這個方程式是橢圓方程式，我們先通過幾個特例來說明其意義。
(1) ф 2 - ф 1 =0，即兩振動同相
這時 x /A1 -y/A2=0
這說明軌跡是一條直線，而且合振動也是簡諧運動，頻率與分振動相同。
(2) ф 2 - ф 1 = π，即兩振動反相
這時 x/A1+ y/A2=0
軌跡仍是一條直線，合振動仍然是簡諧運動，頻率與分振動相同。振動產生的解釋為運動量 。
(3) ф 2 - ф 1 = π /2 ， - π /2
這時 x/A1+y/A2=1
這表示軌跡是一個橢圓。這種情形中，如果兩分振動的振幅相等，則合振動軌跡為圓。
(4) ф 2 - ф 1 等於其它值
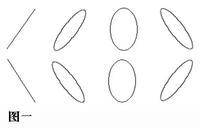四線擺曲線此時合振動軌跡一般是橢圓，其具體形狀（長短軸的方向與大小）合運動的方向由分振動的振幅的大小和相差決定。 下面畫出了 8種不同的情形（如圖一），對應於不同的相差。圖一
