具體要求就是：只用圓規，不許用直尺，在平面上構造四個點，使之成為某個正方形的頂點。當然這個問題後來被證明是有解的。
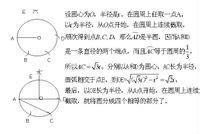
思路：設半徑為1。可算出其內接正方形邊長為√2，也就是說用這個長度去等分圓周。我們的任務就是做出這個長度。六等分圓周時會出現一個√3的長度。設法構造斜邊為√3，一直角邊為1的直角三角形，√2的長度自然就出來了。
具體做法
第一步：找圓心
1 在已知圓周上任取一點A，以A為圓心，適當長為半徑作圓A，交已知圓於兩點B、C。
2 從B點出發，以AB為半徑，在圓A上連續截取3次得到點D。
3 分別以A、D為圓心，CD 為半徑畫弧，兩弧相交於E。
4 以E為圓心，EA為半徑作弧，交圓A於F。
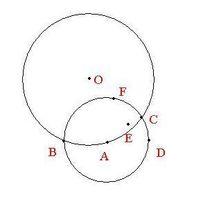四等分圓周5 分別以A、B為圓心，FB為半徑畫弧，兩弧交點O就是所求的已知圓的圓心。
第二步：四等分周長
1 取已知圓O上任一點A，以A為一個分點把⊙O六等分，分點依次為A、B、C、D、E、F。
2 分別以A、D為圓心，AC、BD為半徑作圓交於G。
3 以A為圓心，OG為半徑作圓，交⊙O於M、N，則A、M、D、N即四等分⊙O的圓周。
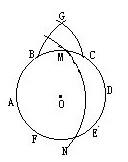四等分圓周第三步：四等分面積
1 以A為圓心，OA長為半徑畫弧，交⊙O於兩點，取⊙O上在點A順時針方向的點為點E。
2 以E為圓心，OA長為半徑畫弧，把點O與點A用圓弧相連。
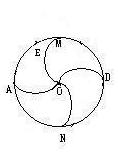四等分圓周3 以同樣的方法作出弧OM、OD、ON，則這四條弧把⊙O面積等分。
