概念
•第一四分位數(Q)，又稱“較小四分位數”，等於該樣本中所有數值由小到大排列後第25%的數字。
•第二四分位數(Q)，又稱“中位數”，等於該樣本中所有數值由小到大排列後第50%的數字。
•第三四分位數(Q)，又稱“較大四分位數”，等於該樣本中所有數值由小到大排列後第75%的數字。
第三四分位數與第一四分位數的差距又稱四分位距（InterQuartile Range, IQR）。
運算過程
關於四分位數值的選擇尚存爭議。
主要選擇四分位的百分比值（p），及樣本總量（n）有以下數學公式可以表示：
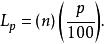四分位數間距情況1: 如果L是一個整數，則取 第L和 第L+1的平均值。
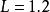四分位數間距情況2: 如果L不是一個整數，則取下一個最近的整數。（比如 ， 則取 2 ）。
四分位距
四分位數間距四分位距（interquartile range, IQR）。是描述統計學中的一種方法，以確定第三四分位數和第一四分位數的分別（即 的差距）。與方差、標準差一樣，表示統計資料中各變數分散情形，但四分差更多為一種穩健統計（robust statistic）。
四分位數間距四分位差（Quartile Deviation, QD），是 的差距的一半，計算公式如下 ：
四分位數間距定義
四分位距通常是用來構建箱形圖，以及對機率分布的簡要圖表概述。對一個對稱性分布數據（其中位數必然等於第三四分位數與第一四分位數的算術平均數），二分之一的四分位距等於絕對中位差（MAD）。中位數是聚中趨勢的反映。
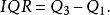四分位數間距相關條目
•四分位數
•百分位數
