簡介
單參數微分同胚群是含一個參數的微分同胚全體構成的群。
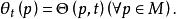單參數微分同胚群設M是微分流形，:M×R→M是光滑映射，對每個t，定義θ:M→M使得若映射族{θ|t∈R}有性質：
1、每個θ都是微分同胚；
2、θ=id；
3、θ∘θ=θ(∀s,t∈R)，則稱是M上一個單參數微分同胚群。
微分同胚
在數學中，微分同胚是適用於微分流形範疇的同構概念。這是從微分流形之間的可逆映射，使得此映射及其逆映射均為光滑（即無窮可微）的。
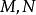單參數微分同胚群
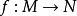單參數微分同胚群
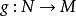單參數微分同胚群
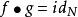單參數微分同胚群
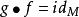單參數微分同胚群
單參數微分同胚群對給定的兩個微分流形，若對光滑映射，存在光滑映射使得、，則稱為微分同胚。此時逆映射是唯一的。
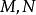單參數微分同胚群
單參數微分同胚群
單參數微分同胚群若在微分流形之間存在微分同胚映射，則稱與是微分同胚的。
微分流形
（differentiable manifold）
微分流形，也稱為光滑流形（smooth manifold），是拓撲學和幾何學中一類重要的空間，是帶有微分結構的拓撲流形。
微分流形是微分幾何與微分拓撲的主要研究對象，是三維歐式空間中曲線和曲面概念的推廣，可以有更高的維數，而不必有距離和度量的概念。
