方法介紹
有限元法是計算固體力學的常用方法,其基本思想是將研究對象解耦成幾個單元分別分析。其中,在對單元體進行力學特性計算的時候,單元剛度矩陣(element stiffness matrix)將力與變形聯繫起來,是非常重要的係數矩陣。
1考慮到應變與位移的關係以及廣義虎克定律,並代入虛功原理,可以得到有限元分析的基本方程:[K]{D}={R}(2)其中,[K]=A[B]T[D][B]J|tdξdη 稱為剛度矩陣,{R}=∫Γ[N]T{F}|J|dξdη 稱為節點載荷向量
2、式中[K]稱為剛度矩陣,{D}為需要求解的節點位移向量,{R}反映的是外界荷載及約束的影響.同其它線彈性結構有限元軟體一樣,鋼岔管有限元程式最終也是歸結為求解該線性代數方程組
剛度矩陣和剛度差不多 就是把剛度變到了多維 比考慮了在多維的情況下 各個維度的相關性。單元剛度矩陣在有限元的概念,把物體離散為多個單元分析,每個單元的剛度矩陣,也就是單元剛度矩陣簡稱單剛。
胡克定律
 單元剛度矩陣
單元剛度矩陣 單元剛度矩陣
單元剛度矩陣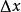 單元剛度矩陣
單元剛度矩陣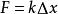 單元剛度矩陣
單元剛度矩陣若彈簧剛度係數為 ,受力為,變形量為,則,這就是著名的胡克定律(Hooke's law)。
剛度是表示物質形變能力的一個量,也就是說物體抵抗變形的能力,其元素值為單位位移所引起的節點力,與普通彈簧的剛度係數具有同樣的物理本質。或者說,是物體產生單位的位移所需要載入的載荷量。剛度矩陣和剛度概念相似,就是把剛度變到了多維 比考慮了在多維的情況下 各個維度的相關性。
在有限元方法中,由於同一變形會由幾個不同的外力產生,而且對一個單元而言外力與位移都可能有多個,分別對應於不同節點,並按照一定的關係耦合在一起,因此可以將胡克定律寫為矩陣的形式。
 單元剛度矩陣
單元剛度矩陣 單元剛度矩陣
單元剛度矩陣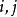 單元剛度矩陣
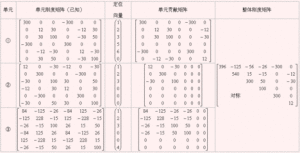
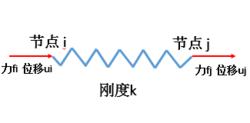
單元剛度矩陣如圖,對於編號為e,兩端自由的彈簧單元,剛度為,兩節點編號分別為。則很容易寫出矩陣形式的胡克定律:
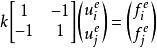 單元剛度矩陣
單元剛度矩陣更一般的形式為:
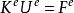 單元剛度矩陣
單元剛度矩陣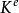 單元剛度矩陣
單元剛度矩陣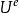 單元剛度矩陣
單元剛度矩陣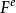 單元剛度矩陣
單元剛度矩陣其中,為單元e的單元剛度矩陣,為節點位移矩陣,為節點力矩陣。
多維問題
 單元剛度矩陣
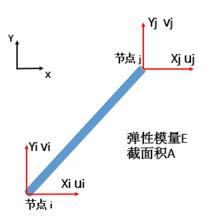
單元剛度矩陣胡克定律可以推廣到任意線性系統,來描述受力與位移的關係,且表達式形式不變。都可用上面的一般形式來表示,但力與位移都可能是多維的。下面,以二維軸力桿件為例,介紹一下多維剛度矩陣 。
 單元剛度矩陣
單元剛度矩陣 單元剛度矩陣
單元剛度矩陣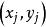 單元剛度矩陣
單元剛度矩陣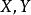 單元剛度矩陣
單元剛度矩陣如圖,為編號e的二維軸力桿件,參數如圖,桿件與x軸夾角為,節點i,j 的坐標分別為和,分別表示x,y方向的力,U,V分別表示x,y方向的位移。
受力後桿件的長度變化為:
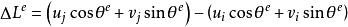 單元剛度矩陣
單元剛度矩陣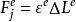 單元剛度矩陣
單元剛度矩陣由彈性力學關係:
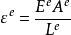 單元剛度矩陣
單元剛度矩陣其中,。
再根據力的分解關係與力的平衡條件:
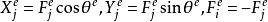 單元剛度矩陣
單元剛度矩陣可以得到力與位移關係矩陣:
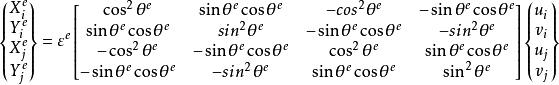 單元剛度矩陣
單元剛度矩陣其中位移矩陣前的係數為多維單元剛度矩陣。
性質套用
由於矩陣的可疊加性,可以由單元的力與位移關係矩陣疊加得到整個系統的關係矩陣,其中位移矩陣前的係數就是整個系統的剛度矩陣。
單元剛度矩陣可以將複雜的力與變形的關係用一個矩陣簡潔直觀的表示出來,從而方便了編程計算,因此,求得單元剛度矩陣是有限元方法解決彈性力學問題的重要步驟之一,具有重要意義。