喬丹–維格納變換

Jordan–Wigner 變換可用於將自旋算符映射到費米子的產生和湮滅算符。一維晶格模型由 Pascual Jordan 與 Eugene Wigner 提出，當前亦得到二維模型的類似變換。 通過把自旋算符變換為費米子的產生湮滅算符，繼而在費米子基矢中作對角化，Jordan–Wigner 變換經常用於精確求解 1D 自旋鏈，例如伊辛模型和 XY 模型。 此變換證明一維空間至少在有些情況下， 自旋-1/2 粒子與費米子不可區別。

自旋與費米子類比

接下來證明如何從一維自旋-1/2粒子構成的自旋鏈映射到費米子。

喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換

將自旋-1/2泡利算符作用到1D鏈的上的第j個晶座，。選取反對易算符, 可以發現, 這些可從費米子的產生湮滅算符中得到。我們可以嘗試，

喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換

這樣，可以得到同晶格上費米子關係, 但對不同的晶格，有關係, 其中, 如此不同晶格上的自旋的對易關係不同於反對易的費米子。人們必須彌補這個問題。

Jordan–Wigner 變換

能夠恢復從自旋算符到真正費米子對易關係的變換於1928由 Jordan 和 Wigner 提出。此為Klein 變換的特殊情況。考慮費米子鏈，定義一組新算符

喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換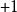
喬丹–維格納變換 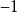喬丹–維格納變換

與之前的定義相差一個相。此相與場模下占據的費米子數有關。如果占有模數為偶，此相等於； 占有模數為奇，相為。表示為

喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換

最後一個等式使用了

這樣，變換後的自旋算符具有正確的費米子對易關係

喬丹–維格納變換 喬丹–維格納變換

逆變換為

喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換
喬丹–維格納變換 喬丹–維格納變換

相關詞條

熱門詞條

聯絡我們