哈達瑪矩陣

哈達瑪（Hadamard)矩陣是由+1和-1元素構成的且滿足Hn*Hn’=nI（這裡Hn’為Hn的轉置，I為單位方陣）n階方陣。

性質

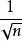哈達瑪矩陣

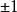哈達瑪矩陣

性質1：H為正交方陣，所謂正交矩陣指它的任意兩行（或兩列）都是正交的。並且行列式為。

性質2:任意一行（列）的所有元素的平方和等於方陣的階數。即：設A為n階由+1和-1元素構成的方陣，若AA‘=nI（這裡A’為A的轉置，I為單位方陣）。

性質3：Hadamard矩陣的階數都是2或者是4的倍數。

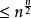哈達瑪矩陣

性質4：若M為n階實方陣，若M的所有元素的絕對值均小於1，則M的行列式，若且唯若M為哈達瑪矩陣時取等。（此結論由哈達瑪不等式得出）

套用

哈達瑪矩陣在信息處理，加工分析中有重要套用（叫做離散的傅立葉分析）。也在通信的編碼領域有相當大的套用。

也可套用在小波變化和量子計算中。