定義
 向量子空間
向量子空間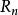 向量子空間
向量子空間 向量子空間
向量子空間設 是 的一個非空子集,若 中的元素滿足:
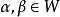 向量子空間
向量子空間 向量子空間
向量子空間(1)若任意的 ,則 ;(對加法是封閉的)
 向量子空間
向量子空間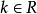 向量子空間
向量子空間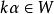 向量子空間
向量子空間(2)若任意的 , (任意實數),則 。(對數乘也是封閉的)
 向量子空間
向量子空間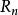 向量子空間
向量子空間則稱集合 是 的一個子空間。
性質
 向量子空間
向量子空間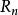 向量子空間
向量子空間 向量子空間
向量子空間如果 是 的一個子空間,則必有 ,即則子空間中必須包含“0向量”。
證明:
 向量子空間
向量子空間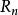 向量子空間
向量子空間 向量子空間
向量子空間 向量子空間
向量子空間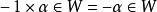 向量子空間
向量子空間是 的子空間, 非空,從而存在 ,由對數乘封閉, ,對加法封閉,所以
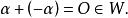 向量子空間
向量子空間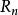 向量子空間
向量子空間 向量子空間
向量子空間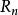 向量子空間
向量子空間此性質是向量子空間的必要條件,如果 中沒有0向量, 就不是 的子空間。而且一般來說,證明向量子空間中有0向量,可以說明子空間非空。
例子
 向量子空間
向量子空間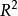 向量子空間
向量子空間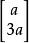 向量子空間
向量子空間 向量子空間
向量子空間 向量子空間
向量子空間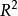 向量子空間
向量子空間例1: 為 中形如 , 為任意實數的集合,驗證 是 的一個子空間。
 向量子空間
向量子空間 向量子空間
向量子空間,所以 非空,任取
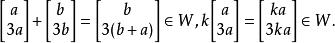 向量子空間
向量子空間 向量子空間
向量子空間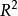 向量子空間
向量子空間故由定義得, 是 的一個子空間。
 向量子空間
向量子空間 向量子空間
向量子空間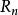 向量子空間
向量子空間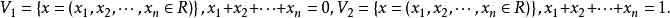 向量子空間
向量子空間例2:設 為全體實數的集合, 是否分別是 的向量子空間,設
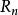 向量子空間
向量子空間規律:凡是對 做一個齊次線性方程的約束的集合都是向量子空間,而作非齊次線性方程的集合則因為它不穿過原點,就不是向量子空間。
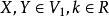 向量子空間
向量子空間證明:任取,設
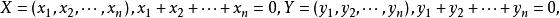 向量子空間
向量子空間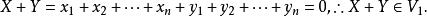 向量子空間
向量子空間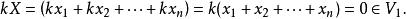 向量子空間
向量子空間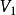 向量子空間
向量子空間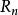 向量子空間
向量子空間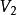 向量子空間
向量子空間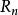 向量子空間
向量子空間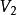 向量子空間
向量子空間故是的向量子空間。而不是的向量子空間。因為0+0+···+0不等於1,因此零向量不屬於。

