基本介紹
用極限,或是中學常用的“微元法”
以圓心為原點,i為x軸上的單位向量 j為y軸上的單位向量
速率為v0
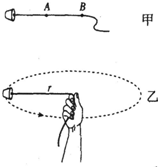 向心力公式推導
向心力公式推導則速度(矢量)
v=v0cosθi v0sinθj
(θ為某點處與x軸的夾角)
又因為θ=ωt
v=v0cosωti v0sinωtj
a=v'=ωv0(cosωti-sinωtj)
|a|=ωv0=rω^2
|F|=m|a|=mrω^2=(mV^2)/r=mvω=(mr4π^2)/T^2=mr4π^2f^2
實例
給你舉個實例來說明吧:
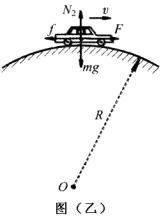
有一輛小汽車通過一個拱橋,小汽車的質量是m,速度是v,拱橋的半徑是r. 小汽車要以一定的速度開過拱橋(這是一部分的圓周運動)吧而不飛起來. 需要怎么樣的條件呢?
請看公式, m越大,F越大. v越大,F也越大.當然,如果汽車質量m越大, 由F=mg得其重力就越大,向心力由重力提供,所以汽車離地而飛起跟質量無關. 汽車開的速度v越快,車也越容易飛起.這時,所需要的向心力F就越大,也就是說拱橋半徑越小,速度越快,汽車就越容易在過拱橋時脫離地面,沿切線方向飛出.
再看公式,r越小,F越大,這就是說.拱橋的半徑r越小,弧度就越大,你想想,比起水平的地面,在上一個特別彎的拱橋的時候,車是不是更容易飛起呢? 這時需要的向心力F也越大.
注意:向心力並不是物體直接受到的力,而是一個物體做保持圓周運動所"需要"的力.在這個例子中,汽車只受到2個力,重力和橋對車的支持力.重力減去支持力就等於車所"需要"的向心力. 不同的車,不同的速度,和不同橋的半徑,車受到的支持力就不一樣.從而導致"重力-支持力=所需要的向心力"也不一樣.
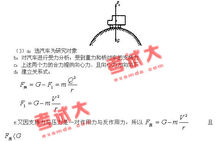 圖例
圖例