簡介
可逆計算(英語:Reversible Computing),是一種計算模型,它的計算過程是可逆的。在這種計算模型中,使用的能量很低,熵的增加會最小化,換句話說,它幾乎不會產生額外的熱。
在可逆計算模型中,轉換函式的前一個狀態,與下一個狀態之間的關係,是一對一的反函式。因此,它的邏輯門,除了產生出我們想要的答案之外,還需要包含許多額外的位元,用以記憶運算的歷史。最早提出可逆計算的先驅,是IBM的工程師羅夫·蘭道爾(Rolf Landauer)。
計算模型
概述
計算模型( computational model)是計算科學中的一個數學模型,它使用大量的計算資源來用計算機模擬研究一個複雜系統的行為。被研究的系統通常是一個複雜的非線性系統,這種系統不易取得簡單、直觀的解析解。相比於推導數學分析來解決問題,它是通過在計算機中調整系統參數並研究實驗結果的差異來完成模型。模型的操作理論可以從這些實驗來推斷/推導。
常見的計算模型有天氣預報模型、地球模擬器模型、飛行模擬器模型、分子蛋白質摺疊模型和神經網路模型。
參見
•人工神經網路
•計算語言學
•決策場理論
•動力系統認知模型
•膜計算
•本體 (信息科學)
•程式語言理論
•微尺度和巨觀模型
轉換函式
轉換函式(英語:Transition function),又譯為 轉換函式,在數學上,它有數種不同的意義:
在拓撲學中,轉換函式是座標卡之間的同胚。假定有兩個座標卡( U, φ) 與 ( U, φ) ,它的轉換函式定義是
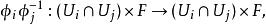 可逆計算
可逆計算對某些集合來說, F被涵蓋在拓撲學中。可參閱纖維叢與圖冊 (拓撲學),來得知更多的細節。在計算理論中,轉換函式意指,一個有限狀態機,或圖靈機,狀態改變的函式。
熵
化學及熱力學中所指的 熵(英語:Entropy),是一種測量在動力學方面不能做功的能量總數,也就是當總體的熵增加,其做功能力也下降,熵的量度正是能量退化的指標。熵亦被用於計算一個系統中的失序現象,也就是計算該系統混亂的程度。熵是一個描述系統狀態的函式,但是經常用熵的參考值和變化量進行分析比較,它在控制論、機率論、數論、天體物理、生命科學等領域都有重要套用,在不同的學科中也有引申出的更為具體的定義,是各領域十分重要的參量。
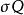 可逆計算
可逆計算熵的概念是由德國物理學家克勞修斯於1865年所提出。克氏定義一個熱力學系統中熵的增減:在一個可逆過程里,被用在恆溫的熱的總數(),並可以公式表示為:
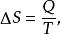 可逆計算
可逆計算克勞修斯對S予以 “熵”(希臘語: εντροπια, entropia,德語: Entropie,英語: entropy)一名,希臘語源意為“內向”,亦即“一個系統不受外部干擾時往內部最穩定狀態發展的特性”。與熵相反的概念為“反熵”(希臘語:εκτροπια,ektropia,源意“外向性”;德語:Ektropie;英語ectropy)。
1923年,德國科學家普朗克來中國講學用到entropy這個詞,胡剛復教授翻譯時靈機一動,把“商”字加火旁來意譯“entropy”這個字,創造了“熵”字,(音讀:低),因為熵是Q除以T(溫度)的商數。
值得注意的是,這條公式只牽涉到熵的增減,即熵一詞只是定義為一個添加的常數。
