概念
在數學上,反比是指兩個變數的乘積為常數時的比例關係:兩個相關聯的量,一個量變化,另一個量也隨著變化,且積不變,這樣他們就是成反比例的量,他們的關係是反比例關係 (就是一個變大另一個變小,變小另一個變大)。比如:①把一個比的前項作為後項,後項作為前項,所構成的比和原來的比互為反比。如9:3和3:9互為反比。②速度和時間成反比,時間和路程是成正比。③只要流通速度不變,單位貨幣的價值恰好與投入流通的貨幣數量成 反比。
兩種相關聯的量,一種量隨另一種量變化而變化,但這兩種量的積一定是個常數,這時,這兩種量是成反比例的量,它們的關係叫做反比例關係。通常用來x的變化規律來表示y的變化規律。
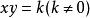 反比定理
反比定理其中,x和y叫做成反比例的量,它們的關係叫做反比例關係,k為常數。
正比與反比
正比定理和反比定理相同之處與聯繫。
正比定理:兩種相關聯的變數,一種量變化,另一種量也隨著變化,如果這兩種量的比值一定那么這兩個數就成正比例,這兩個變數之間的關係就叫做成正比。
相同之處
(1) 事物關係中都有兩個變數,一個常量。
(2)在兩個變數中,當一個變數發生變化時,則另一個變數也隨之發生變化。
(3)相對應的兩個變數的積或商都是一定的。
相互轉化
當正比例中的x值(自變數的值)轉化為它的倒數時,由正比例轉化為反比例;當反比例中的x值(自變數的值)也轉化為它的倒數時,由反比例轉化為正比例。
正比例例子:
1、單價一定,總價和數量成正比例。
2、數量一定,總價和單價成正比例。
3、長方形的長一定,面積和寬成正比例。
4、長方形的寬一定,面積和長成正比例。
5、速度一定,路程和時間成正比例。
6、時間一定,路程和速度成正比例。
7、工作效率一定,工作總量和工作時間成正比例。
8、工作時間一定,工作總量和工作效率成正比例。
9、除數一定,被除數和商成正比例。
10、商一定,被除數和除數成正比例。
11、磚的塊數一定,鋪底面積和每塊磚的面積成正比例。
12、磚的面積一定,鋪底面積和磚的塊數成正比例。
反比例例子:
1、百米賽跑,路程100米不變,速度和時間是反比例;
2、排隊做操,總人數不變,排隊的行數和每行的人數是反比例;
3、做紙盒子,總個數一定,每人做的個數和人數;
4、買東西(實際就用文具用品),總錢數一定,它的單價和數量是反比例;
5、長方形的面積一定,長和寬是反比例;
6、長方體的體積一定,底面積和高是反比例;
7、等分一塊蛋糕,每人分到的蛋糕與人數成反比例;
8、總價一定,單價與數量成反比例;
9、長方體體積一定,底面積與高成反比例;
10、總紙盒一定,每人做的個數與人數成反比例。
套用
反比例關係在套用題中屬於歸總問題。反映在除法中,當被除數一定,除數和商成反比例關係。在分數中,當分數的分子一定,分母與分數值成反比例關係。在比例中,比的前項一定,比的後項與比值成反比例關係。如果再把總數與份數關係具體化為:在購物問題中,總價一定,單價和數量成反比例關係。在行程問題中,總路程一定,速度和時間成反比例關係。在工程問題中,在地上挖個坑所花的時間也(大致地)和雇來挖坑的人數成反比的。
在笛卡爾坐標平面上,兩個具有反比例關係的變數的圖形是一對雙曲線。該圖線上的每一點的 X 和 Y 坐標值之積總是等於比例常數 (k)。由於k非零,所以圖線不會與坐標軸相交。
