反射面天線

由金屬反射面和饋源組成的天線，主要包括單眼射面天線和雙反射面天線兩大類。這是基於光學原理導出的天線形式，廣泛用於微波和波長更短的波段。第二次世界大戰前後多種單眼射面天線開始大量使用，到60年代出現了以卡塞格倫天線為代表的雙反射面天線。

簡介

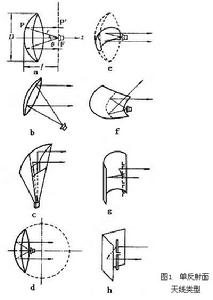
由金屬反射面和饋源組成的天線，主要包括單眼射面天線(圖1)和雙反射面天線（圖3）兩大類。這是基於光學原理導出的天線形式，廣泛用於微波和波長更短的波段。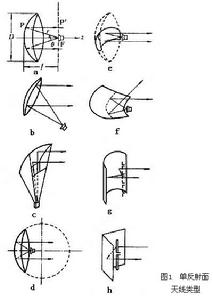

反射面天線

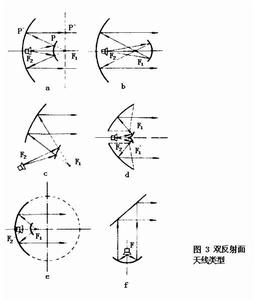反射面天線

　

第二次世界大戰前後多種單眼射面天線開始大量使用，到60年代出現了以卡塞格倫天線為代表的雙反射面天線。它們已成為最常用的一類微波和毫米波高增益天線，廣泛套用於通信、雷達、無線電導航、電子對抗、遙測、射電天文和氣象等技術領域。以衛星通信為例，由於增益高和結構簡單，反射面天線是通信衛星地球站的主要天線形式；由於能製成可展開的折傘形結構，它又是宇宙飛船和衛星天線的基本形式。至今不但已產生了多種多樣的反射面形式來滿足不同的需要，同時也出現了性能優良的多種饋源結構（見天線饋源）。有些還採用組合饋源來形成“和差”波束或多波束（見單脈衝天線和多波束天線）。

單眼射面天線 　

典型形式是鏇轉拋物面天線（圖1a）。它的工作原理與光學反射鏡相似，是利用拋物反射面的聚焦特性。拋物面上點P的以O為原點的柱坐標方程為ρ2＝4fz；以焦點F為原點的球坐標方程為r=2f/(1+cosθ)，f為拋物面的焦距。因此，由焦點F發出的射線經拋物面反射後,到達焦點所在平面的波程為一常數，即。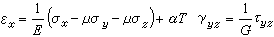

這說明各反射線到達該平面時具有相同相位，因而由饋源發出的球面波經拋物面反射後就變換成平面波，形成沿拋物面軸向輻射最強的窄波束。拋物面直徑D和工作波長λ之比越大，則波束越窄，其半功率點寬度為

2θ0.5＝(58°～ 80°) λ/D

天線增益G與天線開口面（口徑）幾何面積A成正比，而與波長平方λ2成反比，即

G＝4πAη/λ2＝(πD/λ)2η

式中η稱為天線效率或口徑效率，主要由口徑利用係數與截獲係數的乘積決定。口徑利用係數取決於口徑上場分布的均勻程度。當均勻分布（口徑上各點場的相位相同且振幅相等）時，口徑利用係數最大,其值為1。截獲係數是饋源投射到反射面上的功率與饋源總輻射功率之比，理論上最大值也是 1。實際拋物面天線的效率約為0.5～0.7。導致口徑效率下降的因素有：反射面形狀不是嚴格的拋物面；饋源輻射的不是球面波；饋源的輻射不能保證拋物面口徑場等幅分布且使一部分功率從口徑邊沿漏溢；饋源及其支撐桿對口徑的遮擋等。饋源若不準確置於拋物面焦點也會引起口徑效率下降；但有時還有意利用饋源偏離焦點來改變天線波束的指向和寬度。當饋源垂直於拋物面焦軸作上下偏移時，波束最大方向將指向與饋源偏移方向相反的一側；當饋源沿焦軸作前後偏移時，則波束展寬。然而這類偏移不能太大，否則導致波束形狀的嚴重畸變。

圖1b為偏置拋物面天線。其饋源仍置於一鏇轉拋物面的焦點，但只取此拋物面一側的一部分作為反射面而使饋源不會遮擋反射面口徑的輻射，從而改善口徑效率和波束旁瓣特性。另一種偏置結構是喇叭-拋物面天線（圖1c）,它是由一個角錐或圓錐喇叭直接接到偏置拋物面上而成。也可利用球面的一部分作為反射面（圖1d）。饋源通常置於球面半徑R的1/2處，這時饋源所對的小部分球面較接近於以 R/2為焦距的拋物面。由於幾何對稱性，若饋源繞球心鏇轉，可使天線波束在很寬的角域上掃描而形狀基本不變。現代世界上最大的反射面天線是直徑 305米的球形反射面射電望遠鏡。它是固定的，裝于波多黎各島的山谷中，表面用金屬線網鋪織而成，移動懸掛於其上空的饋源可改變波束指向，並依靠地球自轉來掃過360°星空。

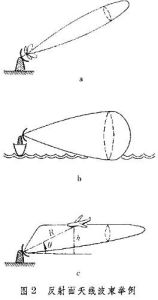反射面天線

上述天線一般具有圓對稱的針狀波束（圖2a）。反射面天線也能形成非圓對稱的波束，如圖2b的扇形波束和圖2c的賦形波束。後者在垂直平面上扇形範圍內的功率方向圖為P(θ)=P0csc2θ(式中θ為仰角)，故稱此賦形波束為餘割平方波束。對空監視雷達和空對地搜尋雷達常採用這種波束，以使等高目標的回波信號是等強度的。只要非對稱地截取鏇轉拋物面的一部分，便可得到扇形波束。若使拋物面天線口徑的垂直尺寸比水平尺寸小（圖1e），則可獲得垂直寬度比水平寬度寬的扇形波束。若直接修改反射面形狀或放置多個饋源，則能產生賦形波束。反射面的水平截線為拋物線而垂直截線修改為一特殊設計的曲線（圖1f），可使反射線向高仰角方向散開，從而形成圖2c的賦形波束。若水平截線為拋物線而垂直截線設計為圓弧，便構成拋物圓環天線。它結合了拋物面和球形反射面的特點，能產生在一個平面內作寬角掃描的窄波束。當水平截線為拋物線而垂直截線取為直線時，則導出拋物柱面天線（圖1g）,它能產生不同垂直-水平比的扇形波束。更簡單的反射面形式是角形反射器（圖1h），它由兩塊平板反射面以夾角α 相交而成，並常用平行金屬棒來代替金屬平板，廣泛用於分米波和米波波段。當夾角α為90°時,角形反射器能把接收信號沿來波方向反射回去，因此常用三塊相互垂直的平板或柵網構成三面體角反射器，用作干擾雷達的假目標。

雙反射面天線 　

典型形式是卡塞格倫天線（圖3a）。主反射面(較大的反射面)為鏇轉拋物面,副反射面(較小的反射面)為凸面,經典形式為雙曲面。這種系統早在1672年就套用於光學望遠鏡,它是利用雙曲面和拋物面的幾何光學特性導出的。圖3a中，由雙曲面兩個焦點F1和F2到雙曲面上任意點P的距離之差為常數,即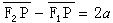。因拋物面的焦點也在F1,根據拋物面性質有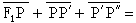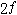。以上二式相加得。

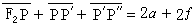因此，由F2發出的射線經雙曲面和拋物面反射後到達口徑平面時其波程為常數，即都具有相同相位。因此雙曲面的存在猶如將來自F2處的球面波變換為以F1為中心的球面波，然後經拋物面反射而變換為平面波向外輻射。副反射面起了把實際焦點由F1移至F2的作用,這可使饋源方便地位於主反射面頂點附近，並且無需長的饋線就能與收發設備相連。為分析方便起見，可把副反射面和饋源看成是一個組合饋源，並用放在F1處的虛饋源來等效。另一方面，也可保持原有饋源不變，而將主、副反射面用單個拋物面來等效，這個等效拋物面的直徑與原來的相同,但焦距增大到Mf,M＝(e+1)/(e-1),稱為放大倍數，其中e為雙曲副反射面的離心率。這樣,拋物面天線的原理和公式，原則上都可套用於雙反射面天線。為提高天線的效率，還可修改副反射面形狀使主反射面口徑場等幅分布，同時也相應修改主反射面形狀以保證口徑場同相。

圖3b為雙反射面天線的另一典型形式，1663年首先用於光學望遠鏡中，稱為格雷果里系統。其主反射面也是鏇轉拋物面，但副反射面為凹面，經典形式是橢球面。橢球面的兩個焦點為F1和F2，由F2發出的球面波經橢球面反射後將變換為中心在F1的球面波，再經過拋物面反射形成平面波。

這兩種雙反射面系統都有偏置形式（圖3c）。1982年用偏置形式的改形卡塞格倫天線獲得了當時最高的反射面天線效率,實測值達0.85。圖3d的雙反射面結構採用偏焦軸的拋物面，但具有軸對稱形式；圖3e為採用球形表面作主反射面的雙反射面天線。另一種雙反射面系統（第二個反射面作用不同）如圖3f，稱為潛望鏡天線。在微波中繼通信中常常需要把天線安裝到幾十米高的鐵塔上。利用這一結構只需把平板反射面架到高塔上，而拋物面及其饋源仍裝在地面附近。