名詞解釋
例如:4321-1234=3087
8730-378=8352
8532-2358=6174
7641-1467=6174
驗證卡布列克運算,任意一個四位數,只要它們各個位上的數字是不全相同的,就有這樣的規律:
(1)將組成該四位數的四個數字由大到小排列,形成由這四個數字構成的最大的四位數;
(2)將組成該四位數的四個數字由小到大排列,形成由這四個數字構成的最小的四位數(如果四個數中含有0,則得到的數不足四位);
(3)求兩個數的差,得到一個新的四位數(高位零保留)。
重複以上過程,最後得到的結果是6174,這個數被稱為卡布列克數。
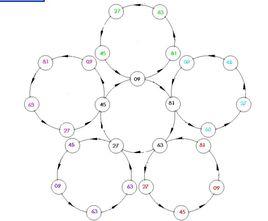
如果K位數也照此辦理,它們不是變成一個數,而是在幾個數字之間形成循環,稱作卡布列克圓舞曲。例如對於五位數54321:
54321-12345=41976
97641-14679=82962
98622-22689=75933
97533-33579=63954
96543-34569=61974
97641-14679=82962
我們把82962 75933 63954 61974稱作循環節,即卡布列克圓舞曲。
相關介紹
卡布列克數是具有以下性質的數:
對於某個<math>X</math>在n進位下滿足以下條件:
<math>X^2 = A n^m + B</math>
<math>X = A + B</math>
其中m是X在n進位下所具有的位數
在二進位下,所有的完全數都是卡布列克數