動態編程

動態編程是在序列分析中經常使用的一種算法技術。在可以使用遞歸，但因為遞歸重複解決相同的子問題造成效率低下的時候，則可以採用動態編程。例如，請看斐波納契（Fibonacci）序列：0, 1, 1, 2, 3, 5, 8, 13, ... 第一個和第二個斐波納契數字分別定義為0和1。第 n個斐波納契數字是前兩個斐波納契數字的和。

動態編程
動態編程是一種在數學和電腦科學中使用的，用於求解包含重疊子問題的最最佳化問題的方法。其基本思想是，將原問題分解為相似的子問題，在求解的過程中通過子問題的解求出原問題的解。動態編程的思想是多種演算法的基礎，被廣泛套用於電腦科學和工程領域。比較著名的套用實例有：求解最短路徑問題，背包問題，專案管理，網路流最佳化等。
概述
動態編程在查找有很多重疊子問題的情況的最優解時有效。它將問題重新組合成子問題。為了避免多次解決這些子問題，它們的結果都逐漸被計算並被保存，從簡單的問題直到整個問題都被解決。因此，動態編程保存遞歸時的結果，因而不會在解決同樣的問題時花費時間。
動態編程只能套用於有最優子結構的問題。最優子結構的意思是局部最優解能決定全局最優解(對有些問題這個要求並不能完全滿足，故有時需要引入一定的近似)。簡單地說，問題能夠分解成子問題來解決。
步驟
最優子結構性質。如果問題的最優解所包含的子問題的解也是最優的，我們就稱該問題具有最優子結構性質（即滿足最最佳化原理）。最優子結構性質為動態規劃算法解決問題提供了重要線索。
子問題重疊性質。子問題重疊性質是指在用遞歸演算法自頂向下對問題進行求解時，每次產生的子問題並不總是新問題，有些子問題會被重複計算多次。動態規划算法正是利用了這種子問題的重疊性質，對每一個子問題只計算一次，然後將其計算結果保存在一個表格中，當再次需要計算已經計算過的子問題時，只是在表格中簡單地查看一下結果，從而獲得較高的效率。
實例
斐波那契數列
計算斐波那契數列的一個最基礎的演算法是，直接按照定義計算：
function fib(n)
if n = 0 or n = 1
return 1
return fib(n − 1) + fib(n − 2)
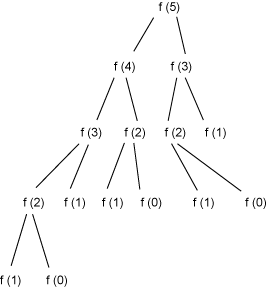
當n=5時，fib(5)的計算過程如下:
fib(5)
fib(4) + fib(3)
(fib(3) + fib(2)) + (fib(2) + fib(1))
((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
(((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
由上面可以看出，這種演算法對於相似的子問題進行了重複的計算，因此不是一種高效的演算法。實際上，該演算法的運算時間是指數級增長的。 改進的方法是，我們可以通過保存已經算出的子問題的解來避免重複計算：
array map [0...n] = { 0 => 0, 1 => 1 }
fib( n )
if ( map( n ) is cached )
return map( n )
return map( n ) = fib( n - 1 ) + fib( n - 2 )
將前n個已經算出的前n個數保存在數組map中，這樣在後面的計算中可以直接易用前面的結果，從而避免了重複計算。演算法的運算時間變為O(n)