預測控制
一般來說,採樣控制算法而非連續控制算法,作為預測控制的表現形式,這是因為計算機是預測控制的實現手段。預測控制,是指利用內部模型的輸出或狀態來進行預測,與此同時,採取反饋校正和有限時域滾動最佳化的思想,對系統的某個性能指標進行最優計算,並且依據這個最最佳化的計算結果來確定一個控制時域內最優的控制序列。
預測控制算法是一種計算機最佳化控制算法,它是基於預測模型來對系統未來輸出進行預測的,結合閉環反饋校正滾動實施最佳化控制。以預測控制的基本原理為基礎,對於同一個系統,可以得到不同的預測控制算法,這是通過採用不同的最佳化策略、模型形式和校正措施實現的。最為常用的三種控制算法分別是動態矩陣控制(DMC)、廣義預測控制(GPC)和模型算法控制(MAC)。
動態矩陣預測控制簡介
動態矩陣預測控制算法(DMC)採用了增量算法,是基於 系統階躍回響的算法,在控制中包含了數字積分環節,對消除系統靜差非常有效,這是DMC算法的顯著優越之處。一般來說,DMC對於弱非線性系統,可先對工作點進行線性化處理,然後按照線性系統的方法進行控制;DMC通常適用於漸近穩定的線性對象,面對不穩定裝置的時候,一般可先用常規PID控制使其穩定,然後再使用DMC算法。
DMC的工作原理框圖如圖1所示。
動態矩陣預測控制的基本原理
預測模型
DMC算法利用先驗信息,建立基於階躍回響的模型,該模型沒有結構限制,較易建立,有很強的功能性,且校正算法簡單,避免了對模型複雜的辨識過程,比較易於在控制器中實現,在階躍回響係數的測取時,可以對被控過程在同一條件下多次測量求取平均值或加權,得到較為精確的預測模型。
 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制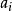 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制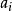 動態矩陣預測控制
動態矩陣預測控制設被控對象單位階躍回響的採樣數據為 。對於漸近穩定的系統,其階躍回響在有限N個採樣周期後將趨於穩態值,即 。因此可用單位階躍回響採樣數據的有限集 合來描述系統的動態特性,該集合的參數便構成了DMC算法中的預測模型參數。系統的單位階躍回響 稱為DMC的模型向量,N稱為建模時域長度,N的選擇應使 (i<N)的值與階躍回響的靜態終值 之差可以被忽略。這裡用動態係數 上面加有“*”來表示實測值或參數估計值。
在k時刻加一控制增量△u(k),在未來N個時刻的模型輸出預測值的矢量形式為(式1):
 動態矩陣預測控制
動態矩陣預測控制其中,
 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制動態矩陣:
 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制式1可化為: 。
由於模型誤差和干擾等的影響,系統的輸出預測值需在預測模型輸出的基礎上用實際輸出誤差修正,即:
 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制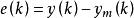 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制其中, ; ; ,h稱為校正參數矩陣。
滾動最佳化
DMC的另一個重要特點是以滾動最佳化來確定系統的控制策略。最優控制律:
 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制由 ,有 ,其中, 為誤差加權矩陣, 為控制加權矩陣。最最佳化指標中的第一項主要用於壓制過於劇烈的控制增量,以防止系統超出限制範圍或發生劇烈震盪。P,M分別為“最佳化時域模型”和“控制時域模型”。
反饋校正
 動態矩陣預測控制
動態矩陣預測控制由於模型誤差、弱非線性特性及其它在實際過程中存在的不確定因素,按預測模型式得到的最優控制規律式不一定能導致系統緊密地跟隨期望值。經過M個時刻後,再重複上述的開環控制算法,那就勢必會造成較大的偏離。此外,這一開環算法不能顧及系統受到的擾動。為了及時糾正這些誤差,必須採用閉環算法。在最優控制規律中,並不將所有M個計算出來的控制增量付諸實踐,而只是實施其中的第一個值,即現時的控制增量 的第一行即可。
控制參數設計
採樣周期T的選取:根據階躍回響,可按T95/T=5~15確定,其中T95是回響曲線上升到穩態值95的時間,針對具體的被控對象,還應考慮到干擾和計算機速度的允許。
 動態矩陣預測控制
動態矩陣預測控制模型時域長度N的確定:模型長度就是廣義對象階躍回響截斷點的點數,它的確定應滿足 。
預測時域長度P和誤差權矩陣Q的選定:預測長度表示從k時刻起,未來多少步的輸出能逼近期望值,P太小,快速性雖好,但穩定性和魯棒性差;P太大,穩定性雖好,但調節作用差。誤差加權矩陣Q反映對不同時刻,輸出逼近期望值的重視程度,一般是對角陣。
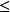 動態矩陣預測控制
動態矩陣預測控制控制時域長度M的選取:控制時域長度表示系統確定未來控制量改變的數口,小的M值有利於控制系統的穩定,但對複雜系統來說,得到的動態性能太差;大的M值則表征允許有較多步的控制增量變化,從而增大控制的靈活性,有較快速的回響,但有可能引起系統不穩定。一般情況下,對於具有簡單動態回響的對象,M=1~2;對於包括有振盪等複雜動態回響的對象,M=4~8。必須注意M P。
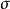 動態矩陣預測控制
動態矩陣預測控制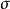 動態矩陣預測控制
動態矩陣預測控制 動態矩陣預測控制
動態矩陣預測控制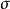 動態矩陣預測控制
動態矩陣預測控制控制權矩陣 的選取: 的主要作用是對△U的變化劇烈程度進行約束,從而限制過大的控制量變化引起對執行器的衝擊。由於控制閥輸入信號有上下限幅,設計時可先讓 ,如果u(k)過大再逐步加入, 一般為對角陣。
另外,校正參數矩陣h反映對象受干擾或模型失配時,預測輸出與實際輸出不一致時的反饋程度。
