定義
公式定義
 加權模式
加權模式 加權模式
加權模式線性動態系統的 加權模式(weighting pattern)是指其輸入 和輸出 之間的關係。假設以下的時變系統
 加權模式
加權模式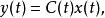 加權模式
加權模式其輸出可以寫成
 加權模式
加權模式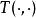 加權模式
加權模式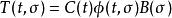 加權模式
加權模式 加權模式
加權模式其中 是系統的加權模式,對此一系統而言,其加權模式為 使得 為狀態轉移矩陣。
加權模式可以決定一個系統,不過若存在一個對應加權模式的實現,也就表示會存在許多個可以對應同一加權模式的實現。
狀態轉移矩陣
狀態轉移矩陣(state-transition matrix)是控制理論中的矩陣,是時間t 和初始時間的函式,可以將初始時間的狀態向量和此矩陣相乘,得到時間t 時的狀態向量。狀態轉移矩陣可以用來找線性動態系統的通解。
線性非時變系統
定義
線上性時不變系統中,其加權模式為:
連續時間系統
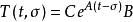 加權模式
加權模式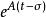 加權模式
加權模式其中為矩陣指數。
離散時間系統
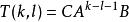 加權模式
加權模式矩陣指數
矩陣指數是方塊矩陣的一種矩陣函式,與指數函式類似。矩陣指數給出了矩陣李代數與對應的李群之間的關係。
設 X為 n× n的實數或複數矩陣。 X的指數,用 e或exp( X)來表示,是由以下冪級數所給出的 n× n矩陣:
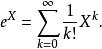 加權模式
加權模式以上的級數總是收斂的,因此 X的指數是定義良好的。注意,如果 X是1×1的矩陣,則 X的矩陣指數就是由 X的元素的指數所組成的1×1矩陣。
線性動態系統
線性動態系統是指其評價函式為線性的動態系統。一般的動態系統不一定存在解析解,但某些簡單的線性動態系統(如線性非時變動態系統),解為解析解,而且存在很多的數學性質。可以計算動態系統在某一平衡點附近的行為,將其近似為線性動態系統,就可以用近似的線性動態系統了解此動態系統的一些特性。
線性非時變系統理論
線性非時變系統理論俗稱 LTI系統理論,源自套用數學,直接在核磁共振頻譜學、地震學、電路、信號處理和控制理論等技術領域運用。它研究的是 線性、非時變系統對任意輸入信號的回響。雖然這些系統的軌跡通常會隨時間變化(例如聲學波形)來測量和跟蹤,但是套用到圖像處理和場論時,LTI系統在空間維度上也有軌跡。因此,這些系統也被稱為 線性時不變平移,在最一般的範圍理論給出此理論。在離散(即採樣)系統中對應的術語是 線性時不變平移系統。由電阻、電容、電感組成的電路是LTI系統的一個很好的例子。
