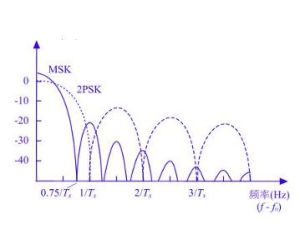
換算方法
信號的功率譜密度若且唯若信號是廣義的平穩過程的時候才存在。如果信號不是平穩過程,那么自相關函式一定是兩個變數的函式,這樣就不存在功率譜密度,但是可以使用類似的技術估計時變譜密度。
f(t) 的譜密度和 f(t) 的自相關組成一個傅立葉變換對(對於功率譜密度和能量譜密度來說,使用著不同的自相關函式定義)。
通常使用傅立葉變換技術估計譜密度,但是也可以使用如Welch法(Welch's method)和最大熵這樣的技術。
傅立葉分析的結果之一就是Parseval定理(Parseval's theorem),這個定理表明能量譜密度曲線下的面積等於信號幅度平方下的面積,總的能量是:
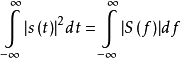 功率譜密度
功率譜密度上面的定理在離散情況下也是成立的。另外的一個結論是功率譜密度下總的功率與對應的總的平均信號功率相等,它是逐漸趨近於零的自相關函式。
相關釋義
功率譜密度譜是一種機率統計方法,是對隨機變數均方值的量度。一般用於隨機振動分析,連續瞬態回響只能通過機率分布函式進行描述,即出現某水平回響所對應的機率。
功率譜密度的定義是單位頻帶內的“功率”(均方值)
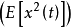 功率譜密度
功率譜密度功率譜密度是結構在隨機動態載荷激勵下回響的統計結果,是一條功率譜密度值—頻率值的關係曲線,其中功率譜密度可以是位移功率譜密度、速度功率譜密度、加速度功率譜密度、力功率譜密度等形式。數學上,功率譜密度值—頻率值的關係曲線下的面積就是均方值
,當均值為零時均方值等於方差,即回響標準偏差的平方值。