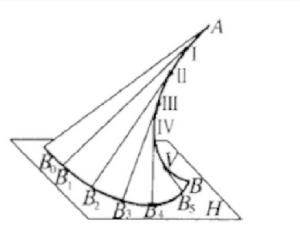
簡介
如圖所示，直母線切一空間曲導線AB於點A，直母線連續運動到素線I B位置，切空間曲導線AB於點I，直母線如此連續運動，並始終保持與曲導線相切所形成的曲面。
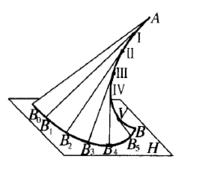切線曲面切線曲面定理
定理1
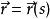切線曲面曲線 的切線曲面上的漸近線為直線或平面曲線
切線曲面證明：曲面的第二基本形式Ⅱ =
由上式知，ds = 0或k = 0或τ = 0。
若ds = 0，則s為常數，v可取任意值，代表的是v—曲線即直母線；若k = 0代表所給的曲線是直線；若τ = 0代表所給的曲線是平面曲線。
定理2
曲線的切線曲面的曲率線為直線或平面曲線。
證明：切線曲面的主方向滿足下面的式子
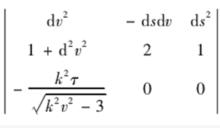切線曲面的主方向化簡得：
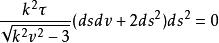切線曲面上式若成立，則下列四種情況：
（1）k=0
（2）τ=0
（3）ds=0
（4）ds+dv=0
其中至少一種是成立的。
若k = 0，則曲線是直線; 若τ = 0，則曲線是平面曲線; 若s = c1，代表的曲線是曲面的直母線; 若ds + dv = 0，即s + v = c2，同樣代表一條直線。
定理3
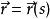切線曲面曲線Γ: 的切線曲面上的腰曲線為曲線本身。
定理4
Bertrand曲線的切線曲面的曲率線為圓。
證明：根據引理1，Bertrand曲線滿足λk + μτ = 1，定理2中的四種情況可分為兩類: (1)k = 0; (2)τ =0，根據曲率和撓率之間的關係，若k = 0，則可得τ= 0。不滿足上述關係式; 若τ = 0，則k為非零常數，k為非零常數的平面曲線為圓，故Bertrand曲線的切線曲面的曲率線為圓。
定理5
兩條達布曲線對的切線曲面在對應點處直母線成固定角。
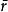切線曲面
切線曲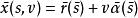面
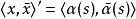切線曲面證明 記兩條曲線分別為r和 ，對應 的 切 線 曲 面 分 別 為：x(s，v)= r(s)+vα(s) ； 對應點處考慮直母線，則s為常數。對v求導得 ，則切線曲面在對應點處直母線成固定角。則切線曲面在對應點處直母線成固定角。
定理6
Bertrand曲線的切線曲面的的極小軌跡為圓。
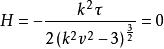切線曲面證明：由H=0知， ，即k=0或τ=0。
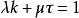切線曲面對Bertrand曲線有 代入有兩種可能：
（1）k= 0時，τ為常數，這種情況不可能存在；
（2）τ= 0時，k為常數，即表明所求軌跡為圓。
定理7
Mannheim曲線的切線曲面的的極小軌跡為直線或圓。
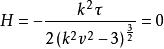切線曲面證明：由H=0知，，即k=0或τ=0。
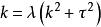切線曲面對Mannheim曲線有，代入有兩種可能：
（1）k= 0時，τ =0，此時表示的曲線是直線；
（2）τ= 0時，k=0或為非零常數，即所求極小軌跡為直線或圓。
