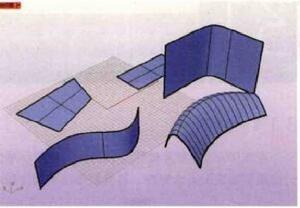
簡介
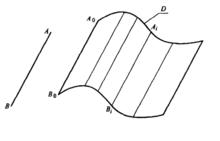曲面的形成一條直線或曲線在空間運動，它所經過的軌跡稱為曲面。我們把形成曲面的這條動線叫做曲面的母線，母線運動中的任一位置稱為曲面的素線。母線在運動時往往要滿足一定的條件，把對母線運動起約束作用的線或面稱為導線或導面。右圖中，母線為直線，起始位置為AB，運動時母線始終平行於直線AB，方向保持不變，A點始終在曲線D上，AB和D就稱為導線。母線運動時的任一位置（如AB）稱為素線。
如果母線按一定規律運動，則形成規則曲面，否則便形成不規則曲面。由直母線形成的曲面稱為直線面，其中，如果連續兩素線（無限接近的相鄰兩素線）共面，稱為單曲面，比如柱面和錐面；否則稱為扭曲面，比如雙曲拋物面。由曲母線形成的曲面稱為曲線面，其中，如果運動時母線的形狀和大小不發生變化，稱為定線曲面，比如球面和環面；否則稱為變線曲面，如三軸橢球面和車身曲面等。
分類
單曲面一般有柱面、錐面、盤旋面三大類。
1．柱面
柱面是鈑金製件中最常用的一種曲面，它的形成如圖所示，直母線AB沿一曲導線D運動，同時始終與導線MN平行，所形成的曲面稱為柱面，其中常見的柱面有兩種，即圓柱面和橢圓柱面（下圖）。
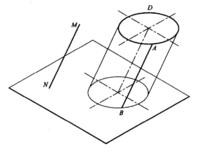柱面的形成當用一與柱面軸線垂直的平面把柱面截斷時，如果交線為圓，則為圓柱面，如果交線是橢圓，則為橢圓柱面。另外，若圓柱或橢圓柱面的底面與其軸線垂直，稱為正圓柱面或正橢圓柱面，否則稱為斜圓柱面或斜橢圓柱面。下圖中，圖a和圖c分別為正圓柱面和斜圓它的形成如右圖所示，直母線AB柱面；圖b和圖d分別為正橢圓柱面和斜橢圓柱面。
2．錐面
錐面是鈑金製件中另一種常用曲面，它的形成如圖所示，直母線沿一曲導線D運動，同時始終通過導線平面外一定點S，所形成的曲面稱為錐面，其中常見的有圓錐面和橢圓錐面。
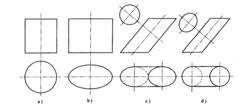圓柱面和橢圓柱面上圖a和c中，因為錐面與垂直於其軸線的平面的交線為圓，所以是圓錐面。圖a中錐底面與軸線垂直，為正圓錐面，而圖c為斜圓錐面。類似地，圖b和圖d分別為正橢圓錐面和斜橢圓錐面。
3．盤旋面
盤旋面可由兩種方法形成。圖中，直母線運動時始終與一空間曲線AB相切，所形成的曲面為盤旋面，AB曲線稱為盤旋面的脊線或回折棱。圖是盤旋面的另一種形成方法，動平面P沿著兩不共面的曲導線AB和CD運動，兩切點Ⅰ和Ⅱ連線的集合也形成盤旋面，這時盤旋面是切平面族的包絡曲面。兩種方法所形成的盤旋面實際上是同一種曲面，它們之間可以互相轉換。
盤旋面在生產中也有著廣泛的套用，比如多種多樣的面板、容器和變形接頭等。
幾何特徵
1、曲面的兩相鄰素線皆為相交直線（或平行直線）。
2、曲面可展開為一平面。
3、曲面一直紋上各點具有公共的切平面，一直紋上各點的法線位於一公共的法平面內。
4、曲面上各點的總曲率為零，即曲面由拋物型點構成。
5、過空間一點S，作直線與曲面的索線平行，則形成該曲面的導錐面。曲面上一素線m的切平面σ與導錐面上對應素線m的切平面σ相互平行。
6、曲面的各素線是曲面上一條曲線的切線（一般情況下），這條曲線L稱為曲面的回折校或脊線。曲面以脊線為界分為兩葉。任一平面ε與曲面的截交線C以脊線上的交面內點K為尖點。
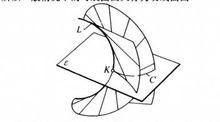切面曲線所以一般情況下的可展曲面又稱為切線曲面。
7、曲面的各索線的切平面構成一個切平面族，它就是曲面脊線的密切平面族。反之，平面作單參數運動形成的平面族，其包絡為一切線曲面，其特徵線即為曲面的脊線。
8、脊線L上一點的漸伸線是一條空間曲線。它位於曲面上，並和曲面各直紋垂直，所以脊線的漸伸線族與直紋組成曲面的正交網。
單曲面的展開
下面研究柱面、錐面和回折棱曲面的展開圖作法。
A．作柱面的展開圖
作柱面展開圖，就象作稜柱側面展開圖一樣，也是用正截面法和側滾法。
在這兩種情況下，柱面用內接於該柱面的稜柱面代替（近似）。下圖1和圖2分別表示用正截面法和側滾法作柱面側表面的展開圖。
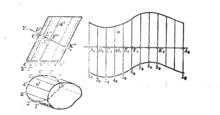圖1作迴轉柱面展開圖，常用正截面法，因為這時不必用稜柱面代替圓柱面。
展開圖上（見圖1）[AA]的長度等於正截面的展開長度。中間點B、C、…、K、…與曲面α各B、C、…、K、…對應，其等分數與柱面正截面圓的等分數相同。這時提高了展開圖的精度，因為不是用近似的柱面解題。
圖2是用側滾法所畫柱面α的側面展開圖。
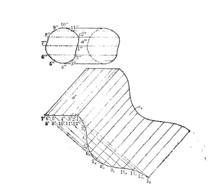圖2B．作錐面的展開圖
求作錐面展開圖的問題，與作稜錐側面展開圖的情況相同，也使用三角形法。為此，錐面用內按於它的稜錐面近似地代替。
圖3表示了內接於已知錐面α的稜錐面SABCDEF…的展開。把圖形SABCDEFA當作錐面的展開圖。內接稜錐的側面數量愈多，錐面的展開實形與近似展開圖之間的差別就愈小。
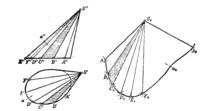圖3如果給出正圓錐表面，則其側面的展開圖是圓的扇形，其半徑等於圓錐面的母線長度l=∣SA∣，中心角
φ =360°r*/l
這裡r ——圓錐底圓半徑。
C．作回折棱面的展開圖
作回折棱面的展開圖同作錐面展開圖一樣採用三角形法。下圖上給出了回折棱面的投影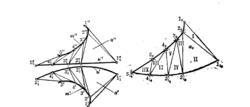（圖4）。
圖4在回折棱m上標出一系列點1、2、3、4、…，過這些點的投影作mˊ和mˊˊ的切線[1 1]、[2 2]、[3 3]、[4 4]、…，在相鄰母線（切線1 1、2 2、3 3、…），所限定的部分曲面內，引對角線2 1、3 2、…，將每個曲線四邊形分為兩個“三角形”。
如果點1和2、2和3、3和4、…之間的距離足夠小，則與頂點1、2、3、…（以及2、3、4、…）相對的“三角形”各邊業可以看作是直線。
為了作出與已知曲面α近似的多邊形曲面的展開圖，我們求出這些三角形各邊的實長。由三角形的三個邊畫出三角形的實形，先由Δ1 21開始，按照圖4的羅馬字的順序依次畫出其它三角形的實形。將1、2、3、…和1、2、3、…各點用光滑曲線連線。圖形α（1234554321）就是曲面伐的近似展開圖。
