內容
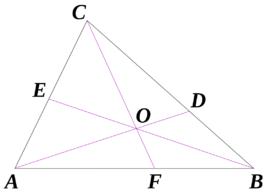
切瓦定理是關於三角形在歐幾里德幾何平面的定理，在三角形 ABC中，將線 AO， BO和 CO從頂點繪製到公共點 O（不在 ABC的一側），以分別在 D， E和 F處遇到相對側，段 AD，BE和 CF稱為切氏線（cevian），然後，使用有符號長度的段 ，
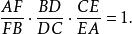切瓦定理換句話說，根據線上的某個固定方向上 A是在 B的左側還是右側，長度 AB被認為是正的或負的。例如，當 F在 A和 B之間時， AF/ FB被定義為具有正值，否則定義為負。
反過來也是如此：如果分別在 BC， AC和 AB上選擇點 D， E和 F，那么
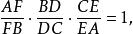切瓦定理然後 AD， BE和 CF是並發的，或者全部三個並行。反過來通常作為定理的一部分。
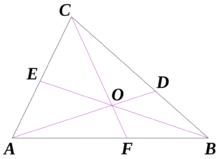圖1.Ceva定理，三條線在ABC內的點O處並發切瓦定理與梅內勞斯定理非常相似，它們的方程式僅在符號上有所不同。
證明
首先，左邊的符號是正的，因為所有三個比率都是正的， O在三角形內部的情況（圖1），或者一個是正的而另外兩個是負的，情況 O是在三角形外面。
要檢查幅度，請注意給定高度的三角形區域與其基準成比例。所以
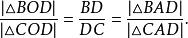切瓦定理因此，
切瓦定理如果 A和 O位於 BC的兩側，則用=號替換-號，得到：
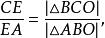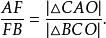切瓦定理
切瓦定理將這三個方程乘以得到：
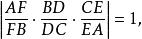切瓦定理使用梅內勞斯定理也可以很容易地證明該定理 ，從三角形 ACF的橫線 BOE，
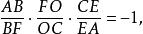切瓦定理從三角形 BCF的橫線 AOD，
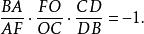切瓦定理該定理遵循這兩個方程式。
反過來作為推論。設 D， E和 F分別線上 BC， AC和 AB上，使得等式成立， AD和 BE在 O點相交， F'是 CO與 AB的交點。然後根據該定理，該等式也適用於 D、 E和 F'，比較兩者可得：
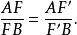切瓦定理但是最多只有一個點可以按給定的比例切割線段，所以 F= F'。
