概述
在計算機科學中,分治法是一種很重要的算法。字面上的解釋是“分而治之”,就是把一個複雜的問題分成兩個或更多的相同或相似的子問題,再把子問題分成更小的子問題……直到最後子問題可以簡單的直接求解,原問題的解即子問題的解的合併。這個技巧是很多高效算法的基礎,如排序算法(快速排序,歸併排序),傅立葉變換(快速傅立葉變換)……
分治法簡介
任何一個可以用計算機求解的問題所需的計算時間都與其規模有關。問題的規模越小,越容易直接求解,解題所需的計算時間也越少。例如,對於n個元素的排序問題,當n=1時,不需任何計算。
n=2時,只要作一次比較即可排好序。n=3時只要作3次比較即可,…。
而當n較大時,問題就不那么容易處理了。要想直接解決一個規模較大的問題,有時是相當困難的。
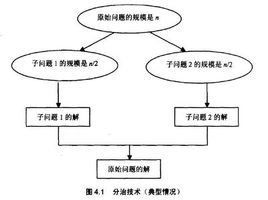
分治法的設計思想是,將一個難以直接解決的大問題,分割成一些規模較小的相同問題,以便各個擊破,分而治之。
分治策略是:對於一個規模為n的問題,若該問題可以容易地解決(比如說規模n較小)則直接解決,否則將其分解為k個規模較小的子問題,這些子問題互相獨立且與原問題形式相同,遞歸地解這些子問題,然後將各子問題的解合併得到原問題的解。這種算法設計策略叫做分治法。
如果原問題可分割成k個子問題,1
分治法所能解決的問題一般具有以下幾個特徵:
1) 該問題的規模縮小到一定的程度就可以容易地解決
2) 該問題可以分解為若干個規模較小的相同問題,即該問題具有最優子結構性質。
3) 利用該問題分解出的子問題的解可以合併為該問題的解;
4) 該問題所分解出的各個子問題是相互獨立的,即子問題之間不包含公共的子子問題。
上述的第一條特徵是絕大多數問題都可以滿足的,因為問題的計算複雜性一般是隨著問題規模的增加而增加;第二條特徵是套用分治法的前提它也是大多數問題可以滿足的,此特徵反映了遞歸思想的套用;第三條特徵是關鍵,能否利用分治法完全取決於問題是否具有第三條特徵,如果具備了第一條和第二條特徵,而不具備第三條特徵,則可以考慮用貪心法或動態規劃法。第四條特徵涉及到分治法的效率,如果各子問題是不獨立的則分治法要做許多不必要的工作,重複地解公共的子問題,此時雖然可用分治法,但一般用動態規劃法較好。
分治法的基本步驟
分治法在每一層遞歸上都有三個步驟:
分解:將原問題分解為若干個規模較小,相互獨立,與原問題形式相同的子問題;
解決:若子問題規模較小而容易被解決則直接解,否則遞歸地解各個子問題;
合併:將各個子問題的解合併為原問題的解。
它的一般的算法設計模式如下:
Divide-and-Conquer(P)
1. if |P|≤n0
2. then return(ADHOC(P))
3. 將P分解為較小的子問題 P1 ,P2 ,...,Pk
4. for i←1 to k
5. do yi ← Divide-and-Conquer(Pi) △ 遞歸解決Pi
6. T ← MERGE(y1,y2,...,yk) △ 合併子問題
7. return(T)
其中|P|表示問題P的規模;n0為一閾值,表示當問題P的規模不超過n0時,問題已容易直接解出,不必再繼續分解。ADHOC(P)是該分治法中的基本子算法,用於直接解小規模的問題P。因此,當P的規模不超過n0時直接用算法ADHOC(P)求解。算法MERGE(y1,y2,...,yk)是該分治法中的合併子算法,用於將P的子問題P1 ,P2 ,...,Pk的相應的解y1,y2,...,yk合併為P的解。
根據分治法的分割原則,原問題應該分為多少個子問題才較適宜?
各個子問題的規模應該怎樣才為適當?
答: 但人們從大量實踐中發現,在用分治法設計算法時,最好使子問題的規模大致相同。換句話說,將一個問題分成大小相等的k個子問題的處理方法是行之有效的。許多問題可以取 k = 2。這種使子問題規模大致相等的做法是出自一種平衡(balancing)子問題的思想,它幾乎總是比子問題規模不等的做法要好。
出處:網路
實踐題目:
給定一個順序表,編寫一個求出其最大值和最小值的分治算法。
分析:
由於順序表的結構沒有給出,作為演示分治法這裡從簡順序表取一整形數組數組大小由用戶定義,數據隨機生成。我們知道如果數組大小為 1 則可以直接給出結果,如果大小為 2則一次比較即可得出結果,於是我們找到求解該問題的子問題即: 數組大小 <= 2。到此我們就可以進行分治運算了,只要求解的問題數組長度比 2 大就繼續分治,否則求解子問題的解並更新全局解
以下是代碼。
*/
/*** 編譯環境TC ***/
#include
#include
#include
#define M 40
/* 分治法獲取最優解 */
void PartionGet(int s,int e,int *meter,int *max,int *min){
/* 參數:
* s 當前分治段的開始下標
* e 當前分治段的結束下標
* meter 表的地址
* max 存儲當前搜尋到的最大值
* min 存儲當前搜尋到的最小值
*/
int i;
if(e-s <= 1){ /* 獲取局部解,並更新全局解 */
if(meter[s] > meter[e]){
if(meter[s] > *max)
*max = meter[s];
if(meter[e] < *min)
*min = meter[e];
}
else{
if(meter[e] > *max)
*max = meter[e];
if(meter[s] < *min)
*min = meter[s];
}
return ;
}
i = s + (e-s)/2; /* 不是子問題繼續分治,這裡使用了二分,也可以是其它 */
PartionGet(s,i,meter,max,min);
PartionGet(i+1,e,meter,max,min);
}
int main(){
int i,meter[M];
int max = INT_MIN; /* 用最小值初始化 */
int min = INT_MAX; /* 用最大值初始化 */
printf("The array's element as followed:\n\n");
rand(); /* 初始化隨機數發生器 */
for(i = 0; i < M; i ++){ /* 隨機數據填充數組 */
meter[i] = rand()%10000;
if(!((i+1)%10)) /* 輸出表的隨機數據 */
printf("%-6d\n",meter[i]);
else
printf("%-6d",meter[i]);
}
PartionGet(0,M - 1,meter,&max,&min); /* 分治法獲取最值 */
printf("\nMax : %d\nMin : %d\n",max,min);
system("pause");
return 0;
}
經典問題
(1)二分搜尋
(2)大整數乘法
(3)Strassen矩陣乘法
(4)棋盤復蓋
(5)合併排序
(6)快速排序
(7)線性時間選擇
(8)最接近點對問題
(9)循環賽日程表
(10)漢諾塔