分數
分數（來自拉丁語，“破碎”）代表整體的一部分，或更一般地，任何數量相等的部分。 當在日常英語中說話時，分數描述了一定大小的部分，例如半數，八分之五，四分之三。 分子和分母也用於不常見的分數，包括複合分數，複數分數和混合數字。
分數表示一個數是另一個數的幾分之幾，或一個事件與所有事件的比例。把單位“1”平均分成若干份，表示這樣的一份或幾份的數叫分數。分子在上，分母在下。
運算法則
1、同分母分數相加，分母不變，即分數單位不變，分子相加，能約分的要約分。
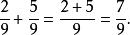分數加法例1：
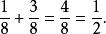分數加法例2：
2．異分母分數相加，先通分，即運用分數的基本性質將異分母分數轉化為同分母分數，改變其分數單位而大小不變，再按同分母分數相加去計算，最後能約分的要約分。
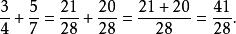分數加法例1：
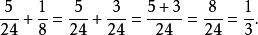分數加法例2：
3．帶分數相加，把各個加數中的整數部分相加所得的和作為和的整數部分，再把各個加數中的分數部分相加所得的和作為和的分數部分，若得的分數部分為假分數，要化為整數或帶分數，並將其整數再加入整數部分；或者把全部加數中的帶分數先化為假分數，再按分數加法的法則求和，然後將結果仍化為帶分數或整數。
4．每次加得的和，都要約分化成最簡分數；如果所得的和是假分數，要化成整數或帶分數。
歷史
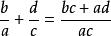分數加法中國是世界上系統敘述分數運算最早的國家，《九章算數》第一章《方田》中，就有比較完整的分數計算方法，將分數加法稱為合分，其法則是：“母互乘子，並以為實，母相乘為法，實如法而一。”實即分子，法即分母，這段話譯為今文是：兩分數的分子與分母交換相乘加在一起作和的分子，而將相乘作和的分母，用現代的符號可寫為。
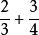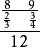分數加法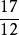
分數加法
分數加法在國外最早建立分數加法運算的是魯多爾夫（Rudolff，C.），他在1530年發表的德文著作中，把加法運算寫成，得。他把公分母12寫在下面，相應的新分子寫在上面，相加得17/12，可見他已掌握了通分的方法。
歐洲直到17世紀，多數的書在計算分數相加時都不要求用最低公倍數。只有溫蓋特（Wingste，E.）所著初等算術課本給出了最小公分母的求法。
