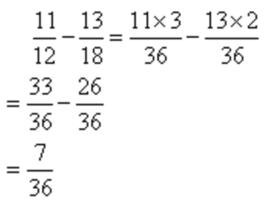基本介紹
分數減法指求兩個分數的差的運算，分數減法是分數加法的逆運算 。
分數減法的運算法則是：
1.同分母分數相減，分母不變，分子相減所得的差作為差的分子。
2.異分母分數相減，先通分，化為同分母的分數後，再按同分母的減法法則進行運算。
3.帶分數相減，先將各帶分數化為假分數，再通分化為同分母的分數，然後按同分母分數相減的法則進行運算，最後的差化為帶分數或整數。
4.差不是最簡分數時，要通過約分化為最簡分數 。
最早的分數減法運算見於中國古代的《九章算術》，該書稱分數減法為減分，其法則是：“母互乘子，以少減多，余為實，母相乘為法，實如法而一。”用現代的數學符號可表示為
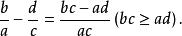分數減法分數減法的法則
在實際計算中，分數減法的法則有以下幾種情況 。
(1)同分母分數相減：分子相減的結果作為分子，原來的分母不變。
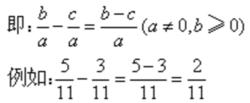分數減法(2)異分母分數相減：先通分，然後按照同分母分數減法的法則進行計算。
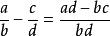分數減法即：(當b、d互質時)
例如：
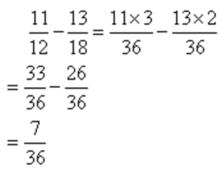分數減法(3)帶分數相減：先把帶分數中的整數部分和分數部分分別相減，然後再把兩部分所得的數合併起來。如果被減數的分數部分小於減數的分數部分，就要從被減數的整數部分里拿出1(在連減時，也有需要拿出2的情況。)化成假分數，與原來被減數的分數部分加在一起，然後再減。
例如：
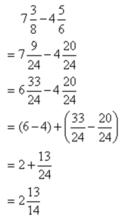分數減法上述三種情況中，如果相減所得的差，不是最簡分數的，要約成最簡分數 。
例如：
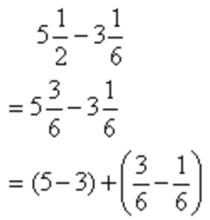分數減法分數減法的運算性質
整數減法的運算性質，也同樣適用於分數減法 。
分數減法套用分數減法的運算性質，可以使一些運算簡便 。
帶分數減整數時，用帶分數的整數部分減去整數，將所得的差與帶分數的分數部分合併在一起，就是最後的結果。
分數減法整數減帶分數時，用整數減去帶分數的整數部分，再減去帶分數的分數部分。通常是先將整數根據減數(帶分數)的情況，也化成帶分數，然後再相減 。
