分層媒質中的波
正文
電磁波和包括聲波在內的彈性波在其中傳播的實際媒質（如大氣、海水、地殼等）都有一個共同特點，即它們的性質在水平方向上的變化比在鉛直方向上的變化慢得多，以致可以把描述它們性質的各個參量近似地看成只是一個坐標（例如鉛直坐標 z）的函式（通常稱為“剖面”），從而使問題大為簡化。具備這種特點的媒質就叫做分層媒質。除上述的平面分層媒質外，還可能存在球面分層（例如考慮到地球的曲率時）和柱面分層等情況。描述分層媒質物理特性的參量對於聲波一般是用波速с，而對於電磁波是介電常數ε。在簡諧波情況下, 這兩種波的行為都由波動方程──亥姆霍茲方程
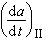
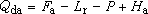
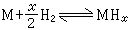或某一“等效波數”。一般的傳播問題就是在給定的剖面k(z)和邊界條件下來求解上述偏微分方程，這時構成特定的本徵值問題，波場由一些本徵函式的加權疊加表出，離散的本徵值所對應的本徵函式稱為簡正波，連續本徵函式的貢獻有時稱為側面波。每個簡正波都有自己的相速、群速、振幅和衰減因數，它們都依賴於頻率，由此產生分層媒質中的頻散效應、波形畸變和多途結構。不難見到，僅在函式k(z)很少幾種形式下才能得到解析解，而在一般情形下不得不求助於數值解。目前已開發出較為成熟的簡正波數值解程式，這種程式的基本運算過程包括對二階常微分方程的差分疊代和邊界條件的擬合。這種程式已經得到廣泛的套用。 上述這種以求解波動方程為基礎的方法通稱為波動法或簡正波方法。如果媒質性質在一個波長範圍內的相對變化很小，就可套用另一種所謂射線法來求解波場。射線法或幾何光（聲）學解是嚴格的波動解的高頻近似，它摒棄了波動圖像，而只關心能流路徑和能流密度。射線在不同媒質的分界面（或同一種媒質的突變面）上發生反射和折射，而在連續的分層不均勻媒質中發生逐漸的彎曲。在普遍情況下，可以利用費馬原理（射線從媒質中一點到另一點所需時間應為極小值）導出射線方程組，並且可以對給定的剖面進行數值積分──射線尋跡。射線法不適用於波場中一些特殊區域，如反轉點（全反射區）附近、焦散面附近以及影區之內，必須加以適當修正。
一般說來，簡正波方法適用於低頻遠場，而射線法適應於高頻近場。近年來對於場的這兩種表述之間的轉換關係作了許多理論研究，簡正波與射線之間所滿足的嚴格變換關係已得到證明。此外，還發展了射線與簡正波混合使用的方法，在此方法中兼收了射線方法和簡正波方法的優點。
波導是分層媒質中存在的一種重要的特殊現象：出現於剖面 k(z)存在極大值的情況下。這時從k取極大值的 z值（稱作波導軸）附近以小於某一角度α 發出的射線將分別在波導軸上、下方發生反轉，因此對應於某一個α 的波的能量就完全被局限在某兩個平面之間，就像是沿著一個以此二平面為壁的“管道”在傳播。對於電磁波來說，地面和電離層下界面就形成這樣兩塊“管道壁”,特別是對於甚低頻範圍內（如3～30千赫）的無線電波，這種波導更具有實際重要性；對於聲波，無論海洋中和大氣中都經常存在波導（聲道）。水下聲道的位置因緯度和季節的不同而異，一般中緯度地區通常位於1 000～1 500米的深度處(見水聲學)，大氣聲道一般有兩個，分別位於約20千米和80千米高度處(見大氣聲學)。至於在地殼中是否存在波導尚未成定論，但從某些跡象來看，至少可以肯定在一定範圍內是很可能存在的。
波在波導中的傳播特性是一個柱面波，即其聲強是與距離的一次方成反比，介於球面波（二次方）和平面波（零次方）之間。由此可見，波在波導中的衰減要比在自由空間中慢得多，這就解釋了許多“超遠傳播”現象（大氣層中的無線電波和次聲波，水下聲道中的聲波等等）。
與波導傳播相反的情況是反波導傳播。在反波導情況下射線不再回到波源所在的水平面,從而形成影區,有時也形成“等效”影區，即影區邊界隨頻率而變，影區內的場一般要用簡正波方法求出，但高頻時可引進衍射線的概念以射線表示。場由單個具有指數衰減特性的簡正波描述。
應當指出，分層模型只是實際媒質的一種近似描述，有一定的適用範圍。對於某些波動傳播問題，還必須考慮媒質更複雜的變化特性。例如某些情況下，特別是在一些地球物理套用中，常會遇到波導性質沿傳播方向變化(即所謂不均勻波導)的情形，這時媒質參量就不再是一個坐標而是兩個以至三個坐標的函式，這在處理上較為困難，現在只對k2=k2(α，z)的幾種特殊情形得到嚴格解。目前，使用拋物近似(PE)方法處理這類問題已得到很大發展。媒質的隨機不均勻性（時間變化和空間變化）對傳播的影響等在特定情況下也是必須加以考慮的。
參考書目
布列霍夫斯基著,楊訓仁譯：《分層介質中的波》,第2版，科學出版社，北京，1984。
伊文等著，劉光鼎譯：《層狀介質中的彈性波》，科學出版社，北京，1966。(W. M.Ewing, et αl., Elstic Wαves in Lαyered Media, McGraw-Hill, New York,1957.)
L. B. Felsen, Hybrid Formulation of Wave Propagation and Scattering, Martine Nijhoff, Dordrecht, 1984.
