簡介
分圓函式域是一類重要的代數函式域,是分圓數域的某種推廣。
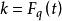 分圓函式域
分圓函式域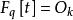 分圓函式域
分圓函式域設 為有限域 F 上單變元 t 的有理函式域,其代數閉包 k 按如下作用形成 上的模:
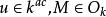 分圓函式域
分圓函式域對 ,定義
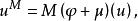 分圓函式域
分圓函式域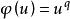 分圓函式域
分圓函式域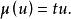 分圓函式域
分圓函式域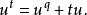 分圓函式域
分圓函式域式中 是k 弗羅尼烏斯自同構, 特別地, 於是
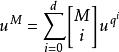 分圓函式域
分圓函式域是 q 次 u 的可分多項式,式中 d 為 M 的次數,
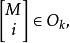 分圓函式域
分圓函式域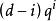 分圓函式域
分圓函式域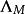 分圓函式域
分圓函式域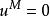 分圓函式域
分圓函式域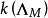 分圓函式域
分圓函式域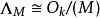 分圓函式域
分圓函式域次數為。若 為 的根集,則 稱為 M 分圓函式域。其在 k 上的伽羅瓦群同構於 的單位群。
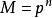 分圓函式域
分圓函式域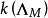 分圓函式域
分圓函式域 分圓函式域
分圓函式域 分圓函式域
分圓函式域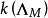 分圓函式域
分圓函式域當 為 d 次首一不可約多項式冪時, 僅在 (P) 和 分歧。類似於克羅內克-韋伯定理,k 的每個在 為順分歧的有限阿貝尓擴張均含於某個分圓函式域的常數域擴張中(順分歧是指分歧指數與 q 互素)。
代數函式域
一個域上的 n(n≥1) 元有理函式域的有限擴張。設 K 是一個在任意域 F 上經添加有限個元素 x,…,x,x,…,x所生成的域,其中 x,…,x(n≥1) 在 F 上是代數獨立的;x,…,x關於 F(x,…,x) 是代數元,則稱 K 是以 F 為係數域的 n 元代數函式域。
當 n=1 時,簡稱 K 為 F 上的代數函式域,記作 K/F 。 K 中所有關於 F 的代數元成一個子域 F┡ ,稱之為 K/F 的常量域。為了方便起見,設 F 本身就是 K/F 的常量域。
