定義
函式極限
函式極限
函式極限
函式極限
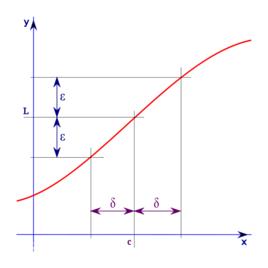
函式極限 函式極限設函式在點的某一去心鄰域內有定義，如果存在常數A，對於任意給定的正數（無論它多么小），總存在正數，使得當x滿足不等式時，對應的函式值都滿足不等式：
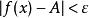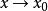函式極限 函式極限
函式極限那么常數A就叫做函式當時的極限，記作
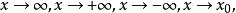函式極限
函式極限概念
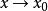函式極限函式極限可以分成 ，而運用ε-δ定義更多的見諸已知極限值的證明題中。掌握這類證明對初學者深刻理解運用極限定義大有裨益。
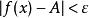函式極限 函式極限 函式極限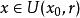 函式極限
函式極限以 的極限為例，f(x) 在點 以A為極限的定義是： 對於任意給定的正數ε（無論它多么小），總存在正數 ，使得當x滿足不等式 時，對應的函式值f(x)都滿足不等式： ，那么常數A就叫做函式f(x)當 x→x。時的極限。
問題的關鍵在於找到符合定義要求的 ，在這一過程中會用到一些不等式技巧，例如放縮法等。1999年的研究生考試試題中，更是直接考察了考生對定義的掌握情況。
如函式極限的唯一性（若極限存在，則在該點的極限是唯一的）
存在準則
有些函式的極限很難或難以直接運用極限運算法則求得，需要先判定。下面介紹幾個常用的判定數列極限的定理。
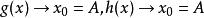函式極限 函式極限
函式極限1. 夾逼定理：（1）當 (這是 的去心鄰域，有個符號打不出）時，有 成立
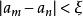函式極限（2） ,那么，f(x)極限存在，且等於A
不但能證明極限存在，還可以求極限，主要用放縮法。
2. 單調 有界 準則：單調增加（減少）有上（下）界的數列必定收斂。
在運用以上兩條去求函式的極限時尤需注意以下關鍵之點。一是先要用單調有界定理證明收斂，然後再求極限值。二是套用夾擠定理的關鍵是找到極限值相同的函式 ，並且要滿足極限是趨於同一方向 ，從而證明或求得函式 的極限值。
3. 柯西 準則
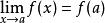函式極限數列收斂的充分必要條件是任給ε>0,存在N(ε),使得當n>N,m>N時，都有 成立。
方法
①利用函式連續性：
（就是直接將趨向值帶入函式自變數中，此時要要求分母不能為0）
②恆等變形
當分母等於零時，就不能將趨向值直接代入分母，可以通過下面幾個小方法解決：
第一：因式分解，通過約分使分母不會為零。
第二：若分母出現根號，可以配一個因子使根號去除。
第三：以上我所說的解法都是在趨向值是一個固定值的時候進行的，如果趨向於無窮，分子分母可以同時除以自變數的最高次方。（通常會用到這個定理：無窮大的倒數為無窮小）
當然還會有其他的變形方式，需要通過練習來熟練。
③通過已知極限
特別是兩個重要極限需要牢記。
④採用洛必達法則求極限
洛必達法則是分式求極限的一種很好的方法，當遇到分式0/0或者∞/∞時可以採用洛必達，其他形式也可以通過變換成此形式。
洛必達法則：符合形式的分式的極限等於分式的分子分母同時求導。
