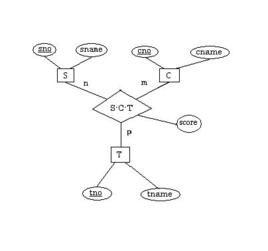
函式依賴
設R(U)是一個屬性集U上的關係模式,X和Y是U的子集。
若對於R(U)的任意兩個可能的關係r1、r2,若r1[x]=r2[x],則r1[y]=r2[y],或者若r1[y]不等於r2[y],則r1[x]不等於r2[x],稱X決定Y,或者Y依賴X。
上面一段話是某些教材上的話,比較不好理解。比如在設計學生表時,一個學生的學號能決定學生的姓名,也可稱姓名屬性依賴於學號,對於現實來說,就是如果知道一個學生的學號,就一定能知道學生的姓名,這種情況就是姓名依賴於學號,這就是函式依賴,函式依賴又分為非平凡依賴,平凡依賴;從性質上還可以分為完全函式依賴、部分函式依賴和傳遞函式依賴。
Y=f(x)
1.數據依賴
在計算機科學中,數據依賴是指一種狀態,當程式結構導致數據引用之前處理過的數據時的狀態。其中最重要的是函式依賴和多值依賴。
2.函式依賴
設X,Y是關係R的兩個屬性集合,當任何時刻R中的任意兩個元組中的X屬性值相同時,則它們的Y屬性值也相同,則稱X函式決定Y,或Y函式依賴於X。
3.平凡函式依賴
當關係中屬性集合Y是屬性集合X的子集時(Y⊆X),存在函式依賴X→Y,即一組屬性函式決定它的所有子集,這種函式依賴稱為平凡函式依賴。
4.非平凡函式依賴
當關係中屬性集合Y不是屬性集合X的子集時,存在函式依賴X→Y,則稱這種函式依賴為非平凡函式依賴。
5.完全函式依賴
設X,Y是關係R的兩個屬性集合,X’是X的真子集,存在X→Y,但對每一個X’都有X’!→Y,則稱Y完全函式依賴於X。
6.部分函式依賴
設X,Y是關係R的兩個屬性集合,存在X→Y,若X’是X的真子集,存在X’→Y,則稱Y部分函式依賴於X。
7.傳遞函式依賴
設X,Y,Z是關係R中互不相同的屬性集合,存在X→Y(Y !→X),Y→Z,則稱Z傳遞函式依賴於X。
函式依賴說明
概念
1. 函式依賴不是指關係模式R的某個或某些關係實例滿足的約束條件,而是指R的所有關係實例均要滿足的約束條件。
2. 函式依賴是語義範疇的概念。只能根據數據的語義來確定函式依賴。
例如“姓名→年齡”這個函式依賴只有在不允許有同名人的條件下成立
3. 資料庫設計者可以對現實世界作強制的規定。例如規定不允許同名人出現,函式依賴“姓名→年齡”成立。所插入的元組必須滿足規定的函式依賴,若發現有同名人存在, 則拒絕裝入該元組。
屬性關係
屬性之間有三種關係,但並不是每一種關係都存在函式依賴。設R(U)是屬性集U上的關係模式,X、Y是U的子集:
● 如果X和Y之間是1:1關係(一對一關係),如學校和校長之間就是1:1關係,則存在函式依賴X → Y和Y →X。
● 如果X和Y之間是1:n關係(一對多關係),如年齡和姓名之間就是1:n關係,則存在函式依賴Y → X。
●如果X和Y之間是m:n關係(多對多關係),如學生和課程之間就是m:n關係,則X和Y之間不存在函式依賴。
案例分析
例: Student(Sno, Sname, Ssex, Sage, Sdept)
假設不允許重名,則有:
Sno → Ssex, Sno → Sage , Sno → Sdept,
Sno ←→ Sname, Sname → Ssex, Sname → Sage
Sname → Sdept
但Ssex -\→ Sage
若 X → Y,並且 Y → X, 則記為 X ←→ Y。
若 Y 不函式依賴於 X, 則記為 X -\→ Y。
在關係模式R(U)中,對於U的子集X和Y,
1.如果 X → Y,但 Y 不為 X 的子集,則稱 X → Y 是非平凡的函式依賴
例:在關係SC(Sno, Cno, Grade)中,
非平凡函式依賴: (Sno, Cno) → Grade。
2.若 X → Y,但 Y 為 X 的子集, 則稱 X → Y 是平凡的函式依賴
平凡函式依賴: (Sno, Cno) → Sno ,(Sno, Cno) → Cno。
3.若 x → y 並且,存在 x 的真子集 x1,使得 x1 → y, 則 y 部分依賴於 x。
例:學生表(學號,姓名,性別,班級,年齡)關係中,
部分函式依賴:(學號,姓名)→ 性別,學號 → 性別,所以(學號,姓名)→ 性別 是部分函式依賴。
4.若 x → y 並且,對於 x 的任何一個真子集 x1,都不存在 x1 → y 則稱y完全依賴於x。
例:成績表(學號,課程號,成績)關係中,
完全函式依賴:(學號,課程號)→ 成績,學號 -\→ 成績,課程號 -\→ 成績,所以(學號,課程號)→ 成績 是完全函式依賴。
5.若x → y並且y → z,而y -\→ x,則有x → z,稱這種函式依賴為傳遞函式依賴。
例:關係S1(學號,系名,系主任),
學號 → 系名,系名 → 系主任,並且系名 -\→ 學號,系主任 -\→ 系名,所以學號 → 系主任為傳遞函式依賴。