簡介
共鳴定理亦稱一致有界性原理或巴拿赫-施坦豪斯定理,是論述有關一族有界線性運算元為一致有界的定理。
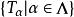 共鳴定理
共鳴定理共鳴定理斷言:設X是巴拿赫空間,Y是賦范線性空間, 是從X到Y的一族有界線性運算元,如果對每個x∈X都有
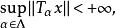 共鳴定理
共鳴定理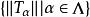 共鳴定理
共鳴定理則數集 是有界的。
發展
共鳴定理是泛函分析中的一條重要定理,它是由巴拿赫(Banach,S.)與施坦豪斯(Steinhaus,H.D.)於1927年在勒貝格(Lebesgue,H. l.)關於奇異積分、特普利茨(Toeplitz,O.)關於正則求和法以及哈恩(Hahn,H.) 關於插值理論等前人研究成果的基礎上提出的。
有界線性運算元
有界線性運算元是泛函分析中一種重要的運算元。
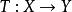 共鳴定理
共鳴定理 共鳴定理
共鳴定理 共鳴定理
共鳴定理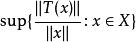 共鳴定理
共鳴定理 共鳴定理
共鳴定理 共鳴定理
共鳴定理 共鳴定理
共鳴定理 共鳴定理
共鳴定理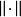 共鳴定理
共鳴定理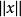 共鳴定理
共鳴定理 共鳴定理
共鳴定理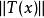 共鳴定理
共鳴定理 共鳴定理
共鳴定理設是從線性賦范空間到的線性運算元。 如果當存在且有限,則稱是有界線性運算元,也就是說將中的每個有界集映射為中的有界集。此處|表示範數,表示中定義的範數,表示中定義的範數。
