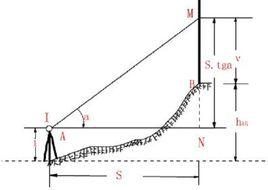
簡介
計算方式
在使用電子測距方式進行三角高程測量時,對直接測得的高差加入兩差改正數得到改正後高差:
h'=h+f
式中:h'——改正後高差;
h ——直接觀測所得高差;
f ——單項觀測高差的兩差改正數。
兩差改正數f按下式計算:
f=(1-K)*D^2/(2R)
式中:K——大氣垂直折光係數;
D——直接觀測時兩點間的水平距離;
R——地球平均曲率半徑,一般採用值為R=6371km。
兩差改正係數C的確定方法
針對低標(近地面)三角高程測量“兩差”改正係數C在實際工程中無已知且合理的數值可以採用的問題,推證出了一種可根據實際工程的觀測數據確定C值的方法,並可據此合理評定三角高程測量觀測成果的精度。
對於坡度較大的測區,三角高程測量仍是高程控制測量的主要方法。根據現行測繪規範的要求,採用三角高程測量方法進行高程控制測量時,一般同一條邊上應進行對向觀測(也稱為直反覘觀測,下同)。為保證必要的觀測精度,同一條邊上所進行的對向觀測應計算高差較差,並與規範的限差值進行比較,超限者需要返工重測;當邊長較長(例如大於300m)時,應對直覘及反覘觀測高差先分別加入“兩差”改正數f,求得改正後高差 。
(1)用該測區以往測定的K值。
(2)工程開工前夕,在測區內兩已知水準點間進行精密三角高程測量,以確定該測區這一時期的K值。
(3)利用三角高程測量中未經“兩差”改正的對向觀測高差值計算測區內的平均K值。
採用上述各種方法有些測繪教科書中推薦的K= 0.14(全國平均值)相比,對於外業中對向觀測邊三角高程測量高差較差的計算,均可起到不同程度的較好效果,返工現象有所減少,觀測精度能夠達到要求,甚至有所提高。這說明,選取K值,用實測數據計算比選用K= 0.14要有利得多。
三角高程測量外業觀測中K的選取問題。那么,在進行三角高程路線(網)的平差計算之前,是否有必要根據對向觀測高差推求合理的K值呢?其原因如下:
(1)進行三角高程路線(網)的平差計算之前,可根據對向觀測高差推求出一個合理的K值或C值用於計算各個對向觀測邊的直反覘高差較差,以其與規範的限差進行比較,可避免外業中因K值或C值選用不合理而出現的直反覘高差較差超限導致盲目重測問題,並可據此求得一組對向觀測高差的中誤差,用其最小值評定對向觀測高差的質量;而利用預選的K值所推求的一組對向觀測高差的中誤差的最小值去評定對向觀測高差的質量不盡合理。
(2)進行三角高程路線(網)的平差計算之前,根據對向觀測高差推求出的一個合理的K值或C值,可作為以後該測區該季節(或者同類觀測條件下)進行三角高程測量外業選用K值或C值的參考值,對於接續的用光電測距儀測距的地形測圖工作,當測距邊較長時,更具有直接使用價值。
確定三角高程測量“兩差”改正係數C的方法 ,是以一組對向觀測邊觀測高差的較差的中誤差最小為前提的。用此法確定C時,對向觀測邊不宜太少。這是因為中誤差本身是從機率統計觀點出發定義的,若對向觀測邊太少,所確定的三角高程測量“兩差”改正係數C將與實際工程不符,甚至可能出現相反的情形。