全密點

簡介

全密點亦稱密集點，是反映勒貝格可測集中的點在一點附近高度密集情況點概念。

勒貝格可測點集E中幾乎每個點都是它的全密點，當E⊂R的情形這是勒貝格(Lebesgue,H.L.)最早證明的。

定義

密度

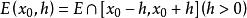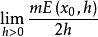全密點

全密點

設E是R中勒貝格可測集，對於任意一點x，記，如果極限存在，則稱它為E在點x處的密度。

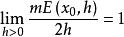全密點

全密點

如果E在點x處的密度等於1，即，則稱x為E的全密點。

套用

可測集E中幾乎所有的點都是E的全密點。

有了全密點、全密性的概念後，可對函式連續概念作一個重要的擴充。

勒貝格可測集

勒貝格可測集是實變函式論的重要概念之一，指勒貝格意義下可求“長度”、“面積”或“體積”的一類集合。

若m*為R 上的(L)外測度，E⊂R 且滿足卡拉西奧多條件，即對任意點集T⊂R ，有

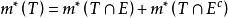全密點

則稱集E為勒貝格可測集，簡稱(L)可測集。