簡介
在數學方面,特別是在類別理論領域,內射對象的概念是內射模概念的泛化。 這個概念在同倫論和模型類理論中是很重要的。 另一個概念是投影對象。
定義
定義C是一個類,讓H成為C的一類態射。
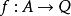 內射對象
內射對象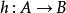 內射對象
內射對象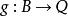 內射對象
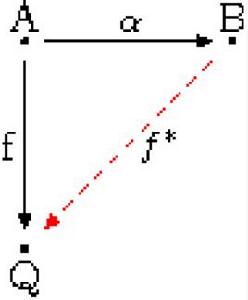
內射對象如果對於每個態射 ,以及H中的每個態射: ,存在一個態射 可以將H傳遞到f,這樣,C中的對象Q被認為是注入了H,表示為
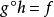 內射對象
內射對象上述定義中的態射g不需要由h和f唯一確定。
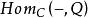 內射對象
內射對象在一個小類別中,這相當於要求hom 函子 承載著H態射。
H的類選擇是單態的類,在這種情況下,內射對象的表達就被使用到了。
阿貝利例子
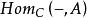 內射對象
內射對象阿貝爾例子是內射概念的原始框架(仍然是最重要的一個例子)。 如果C是一個阿貝爾類,則C的對象A是內射如果它的函子 是準確的。
讓
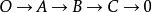 內射對象
內射對象在C中是一個確切的順序,這樣A就是內射的。 那么若且唯若C是內射的時候,序列就會發生分裂並且B也是內射的。
充足的內射
讓C成為一個類,H是C的一類態射;如果從X到H的內射對象中存在一個H態射的話,那么對於C類中的每個對象X都有充足的H態射。並且,H通常是單態的類,並且對於C的每個對象X具有足夠的內射,存在來自X的單態 到一個內射對象。
內射體
如果對於任何態射f,僅當f在H中時,複合f也在H中,那么在C中的H形態g被稱為重要的H。如果H 是單態的類,g被稱為重要的單態。
如果f是具有域X和H內射密碼子,則將G稱為X的H內射體。這種H內射體是唯一的。
舉例
(1)在阿貝爾群和群同態的類中,內射對象是一個可分割的群。
(2)在模和模同態的類中,R-Mod是一個內射模。 R-Mod具有內射體。
(4)在度量空間和非擴展映射的類別中,內射對象是內射度量空間。
(5)在T0空間和連續映射的類中,內射對象始終是連續格上的Scott拓撲,因此總是局部緊湊。
(6)在簡單集合的類別中,關於無限擴展類的內射對象是Kan複合體。
(7)另外還討論了更一般類別中的內射對象,例如在某些環形空間(X,O)上的函式類別或OX模組的滑輪類別中。