簡介
光彈性描述了在機械變形下材料的光學性質的變化。 它是所有介電介質的特性,通常用於實驗確定材料中的應力分布,其中給出了材料不連續性周圍的應力分布圖。 光彈性實驗是確定材料中臨界應力點的重要工具,用於確定不規則幾何形狀的應力集中。
光彈性(英語:Photoelasticity)是某些透明材料(主要是塑膠、玻璃、環氧樹脂等非晶體)在承受載荷出現應變的狀態下由各向同性變成各向異性並展現出對光的雙折射的現象。基於這種材料性質發展出的描繪物體應力應變分布的試驗物理學方法稱為光測彈性學。相比於應力-應變的分析學方法(數學方法)的局限,光彈性法對於描繪複雜幾何結構以及複雜載荷下的物體的應力應變尤其有效,即使對於材料的突然斷裂處也能夠給出相對準確的應力分布圖像,是用於檢測臨界應力點和應力集中的重要方法。
此法的主要特點是在進行三維光彈性實驗應力分析時不必破壞模型,有時也可不將模型凍結。1939年,R.韋勒首先提出光彈性散光法,經過D.C.德魯克、H.T.傑索普、M.M.弗羅赫特等人的努力,到50年代末,它的原理已比較完善,但由於技術上的原因,這種方法未得到廣泛使用。60年代雷射技術的發展,獲得高強度的片光源,才使光彈性散光法得到推廣。此法已用來解決扭轉、平面應力、表面應力和軸對稱應力等的測量問題,但尚難以用於研究較複雜的三維應力問題。
歷史
光彈性現象由蘇格蘭物理學家大衛·布儒斯特第一次記錄,並在二十世紀初由E.G.Coker和倫敦大學的L.N.G. Filon發展套用。 他們的著作《光彈性論》(Treatise on Photoelasticity )由劍橋大學出版社在1930年出版並成為該學科的標準手冊。在1930到1940年間,俄語、德語和法語的許多其他著作先後出版。同時該領域不斷取得新的進展,大量的技術改進和簡化得以實現。光測彈性力學的測量範圍擴展到三維應力,並越來越流行,許多光彈性實驗室得到建立。使用發光二極體的數字偏光鏡的出現,使得連續監測處於負載下的物理結構成為可能,促進了動態光彈性技術的發展。動態光彈性技術對於例如材料斷裂等方面的複雜現象研究起到了重大作用。
原理
光線通過各向同性的透明介質時,由於介質中的微粒或分子的作用,產生散射光。垂直於傳播方向的散射光,是平面偏振光。它的光強度和入射光的性質、材料的散光性能以及觀察方向有關。入射為自然光時,在傳播軸的所有垂直方向的散射光的光強度相等。
光彈性是基於一些透明材料的雙折射現象。雙折射是指光線透過材料時表現出兩種不同的折射率,在許多晶體中可以觀察到這種現象。在光測彈性過程中,光彈性材料的某一點的折射率大小跟該點的應力狀態直接相關。通過偏光器分析雙折射,可以得到諸如最大切應力及其方向等信息。
當一束電磁波通過光彈性材料時,它的電磁波分量沿著材料兩個主應力的方向被分解,並且由於雙折射表現出不同的折射率,折射角的不同導致兩束光分量產生相位差(一束延遲於另一束)。構想一片很薄的各向同性材料試樣,在二維光測彈性狀態下,相位延遲的大小由光學應力定理( stress-optic law)給出:
其中Δ是相對延遲, C是光學應力常數( stress-optic coefficient), t是樣本厚度,λ是光的波長,σ和σ分別是兩個主應力。相對延遲改變了透射光線的偏振方向,偏振器在光線通過試樣之前和之後講兩個偏振方向不同的光線分量結合起來。由於光線的相互干涉,干涉圖樣得到顯示。干涉圖樣的序號 N被定義為:
其跟相對延遲量有關。通過研究干涉圖樣,材料各處的應力狀態可以根據計算得到。即使對於不表現出光彈性性質的材料,也可以研究其應力分布:只要用光彈性材料製成相同幾何結構的模型,並施加相同的載荷,就可以對其真實的應力分布進行研究。
公式定義
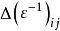 光彈性
光彈性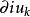 光彈性
光彈性對於線性介電材料,反介電常數張量的變化 相對於變形(位移的梯度) 被描述成:
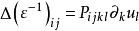 光彈性
光彈性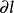 光彈性
光彈性其中P是第四級光彈性張量,u是平衡的線性位移, 表示相對於笛卡爾坐標x的區分。 對於各向同性材料,該定義簡化為
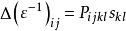 光彈性
光彈性其中P是光彈性張量的對稱部分,s是線性應變。P的反對稱部分被稱為旋轉光張。 從任何一個定義來看,很明顯的是,變形可能引起光學各向異性,這可導致另外的光學各向同性材料表現出雙折射。
彈性分析
光測彈性法在二維和三維的應力狀態下都可以得到套用。三維的光彈性分析跟二維有著密切的關係,所以二維光測彈性的研究非常重要。二維光測彈性,也稱為平面光測彈性,的試驗對象是一個厚度遠小於其長度和寬度的平板試樣(一般來說應小於十分之一),這樣一來在平面以外方向上的應力可以忽略為零,只考慮平面長寬方向上的應力變化。分析試驗的儀器多種多樣,最為基本的是平面偏光器和圓形偏光器。
二維光測彈性試驗的目的是測量出沿著兩個主應力方向分解的兩束光的相對延遲大小,由此計算出相對的主應力和其方向。主應力的具體數值由應力分解給出。有數種不同的理論和試驗方法可以幫助解出每個獨立的應力分量。
實驗原理
實驗程式依賴於某些透明材料所顯示的雙折射性質。雙折射是通過給定材料的光線經歷兩個折射率的現象。在許多光學晶體中觀察到雙折射(或雙折射)的性質。在施加應力時,光彈性材料表現出雙折射的性質,並且材料中每個點處的折射率的大小與該點處的應力狀態直接相關。通過用稱為偏振器的儀器分析雙折射,可獲得諸如最大剪下應力及其取向的信息。
當光線通過光彈性材料時,其電磁波分量沿著兩個主應力方向分解,並且由於雙折射,每個部件經歷不同的折射率。折射率的差異導致兩個組分之間的相對相位延遲。假設由各向同性材料製成的薄樣品,其中二維光彈性適用,相對延遲的幅度由應力 - 光學定律給出:
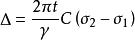 光彈性
光彈性其中Δ是感應延遲,C是應力光學係數,t是樣品厚度,γ是真空波長,σ1和σ2分別是第一和第二主應力。 延遲改變透射光的極化。 偏振器在通過樣品前後結合了光波的不同極化狀態。 由於兩個波的光學干涉,顯示出條紋圖案。 條紋數N的數字表示為
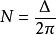 光彈性
光彈性這取決於相對遲滯。 通過研究邊緣圖案,可以確定材料中各個點處的應力狀態。
對於不顯示光彈性行為的材料,仍然有可能研究應力分布。 第一步是建立一個使用光彈材料的模型,其具有類似於正在研究的實際結構的幾何形狀。 然後以相同的方式施加負載,以確保模型中的應力分布與實際結構中的應力相似。
套用
光彈模型驗證加筋模型。在光彈性兩部分環氧樹脂中鋼板片周圍的等色條紋圖案。
光彈性已經用於各種應力分析,甚至用於設計中的常規套用,特別是在數值方法出現之前,例如有限元或邊界元素。Polariscopy的數位化可以實現快速的圖像採集和數據處理,從而允許其工業套用控制諸如玻璃[4]和聚合物等材料的製造工藝的質量。牙科利用光彈性分析假牙材料的應變。
光彈性可以成功地用於研究砌體內的高度局部應力狀態或嵌入彈性介質中的剛性線夾雜物(加強筋)附近在前一種情況下,由於磚之間的接觸,問題是非線性的,而在後一種情況下,彈性解是奇異的,因此數值方法可能無法提供正確的結果。這些可以通過光彈技術獲得。利用與高速攝影相結合的動態光彈性來研究材料中的斷裂行為光彈性實驗的另一個重要套用是研究雙材料缺口周圍的應力場,雙材料缺口存在於諸如焊接或粘合結構的許多工程套用中。
二維光彈性
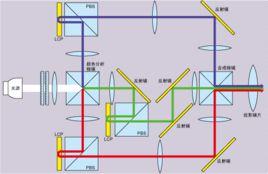
光彈性可以描述三維和二維應力狀態。然而,檢查三維系統中的光彈性比二維或平面應力系統更為重要。因此,本節介紹了平面應力系統中的光彈性。當原型的厚度與平面中的尺寸相比要小得多時,就達到了這個條件。因此,只關心與模型平面平行的應力,因為其他應力分量為零。實驗設定因實驗而異。使用的兩種基本設定是平面偏振鏡和圓形偏振鏡。
二維實驗的工作原理允許測量延遲,其可以轉換為第一和第二主應力及其取向之間的差。為了進一步獲得每個應力分量的值,需要一種稱為應力分離的技術[17]利用幾種理論和實驗方法來提供額外的信息來解決單個應力分量。
平面偏振器設定
該設定由兩個線性偏振器和光源組成。 根據實驗,光源可以發射單色光或白光。 首先,光通過第一偏振器,其將光轉換成平面偏振光。 該裝置以這樣的方式設定,使得該平面偏振光然後通過應力樣本。 然後,在樣品的每個點,然後遵循該光在該點處的主應力的方向。 然後使光通過分析儀,我們終於得到邊緣圖案。
平面偏光鏡設定中的邊緣圖案包括等色譜和異色性。 異構體的變化隨著偏光鏡的方向而發生變化,而同位素沒有變化。
圓偏振器設定
在圓形偏振鏡設定中,將兩個四分之一波片添加到平面偏振器的實驗裝置中。 將第一個四分之一波片放置在偏振片和樣品之間,第二個四分之一波片放置在樣品和分析儀之間。 在源極偏振器之後添加四分之一波片的效果是我們得到通過樣品的圓偏振光。 分析儀側四分之一波片在光通過分析儀之前將圓偏振狀態轉換回線性。
圓偏振器在平面偏光鏡上的基本優點是,在圓形偏振鏡設定中,我們只得到等色譜,而不是等色譜。 這消除了異色素和異色素之間的區分問題。