基本介紹
優美標號的研究始於20世紀60年代,研究的中心問題是哪些圖是優美圖,至今尚無一般方法來判斷一個圖是否是優美圖,僅知道很少一部分圖是優美圖。
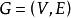 優美標號
優美標號設是p個頂點q條邊的簡單圖 。
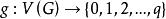 優美標號
優美標號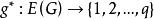 優美標號
優美標號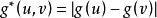 優美標號
優美標號定義1 設是單射,若g的誘導映射是雙射,,則稱g是G的一個 優美標號(graceful labeing),並稱G是一個優美圖。
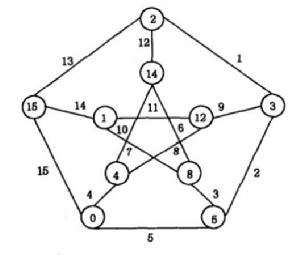
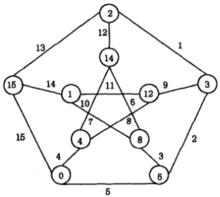 圖1
圖1 優美標號
優美標號例如圖1給出了彼得森(Petersen)圖的一種優美標號。
關於優美標號的主要結論
關於優美標號的主要結論:
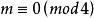 優美標號
優美標號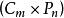 優美標號
優美標號1.當m,n為偶數或時,是優美的(Jungreis和Reid)。
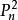 優美標號
優美標號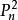 優美標號
優美標號2.對於任意正整數n≥3,是優美的(梁志和)。這裡是指路P上所有距離為2的點之間再連一條邊而得到的圖。
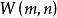 優美標號
優美標號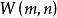 優美標號
優美標號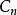 優美標號
優美標號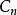 優美標號
優美標號3.蛛網圖是優美的(1980年,Koh)。這裡 是指具有同心O的m個圈,從O發出的射線將O與每個上相應的點連線得到的圖 。
關於優美標號的主要猜想
關於優美標號的主要猜想:
1) 所有的樹是優美的(1963年,Ringel和Kotzig),其子猜想是:所有的龍蝦樹(樹去掉1度點後成的毛毛蟲)是優美的(1979年,Bermord)。(尋找不優美的樹至今未果)。
 優美標號
優美標號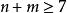 優美標號
優美標號2)優美的充要條件是,(Frucht和Salinas).
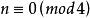 優美標號
優美標號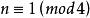 優美標號
優美標號3) 當或時,n塊三角仙人掌是優美的(Rosa),這裡三角仙人掌是指所有塊皆為三角形的連通圖。
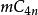 優美標號
優美標號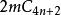 優美標號
優美標號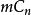 優美標號
優美標號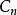 優美標號
優美標號4) 對自然數m,n,圖和是優美的(1984年,Kotzig),這裡是m個圈的不交並。
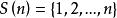 優美標號
優美標號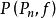 優美標號
優美標號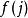 優美標號
優美標號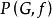 優美標號
優美標號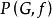 優美標號
優美標號5)1983年Lee猜想:對任意n>1和圖G的頂點集上置換f,f-置換圖是優美的。(這裡P是有n個點的路,f-置換圖是指:若G和G是G的2個不交的拷貝,f是G的頂點集S(n)上置換,將G中的每個點j與G中點連邊而得到的圖,記為。1994年Lee等進一步猜想:若G是具有n個點的優美圖,但不是二分圖,則對S(n)上任意置換f,是優美的。
對上述猜想目前均未獲徹底解決,已經知道的主要結果有:
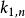 優美標號
優美標號1)路P和星形圖是優美的;毛毛蟲(樹去掉1度點後形成的一條路或平凡圖)是優美的;具有至多27個點的樹是優美的等等。一些由較小優美樹構造較大優美樹的方法。
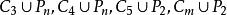 優美標號
優美標號2)優美性已經解決;當
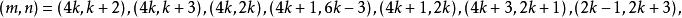 優美標號
優美標號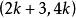 優美標號
優美標號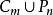 優美標號
優美標號和時,是優美的。
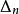 優美標號
優美標號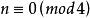 優美標號
優美標號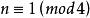 優美標號
優美標號3)已經證明對於荷蘭風車圖(m個三角形恰有一個公共點的圖),三角蛇(即塊割點圖為一條路的三角仙人掌),當或時是優美圖。
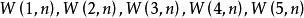 優美標號
優美標號4)康慶德等人證明了對所有n≥3都是優美的。
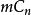 優美標號
優美標號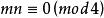 優美標號
優美標號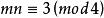 優美標號
優美標號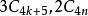 優美標號
優美標號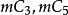 優美標號
優美標號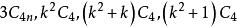 優美標號
優美標號5)優美的必要條件是或;k≥1時是優美的;m≥2時均是不優美的;還有更進一步的結果:不但具有優美標號,而且還具有更強的標號——平衡標號。
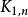 優美標號
優美標號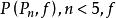 優美標號
優美標號6)已知優美置換圖有:當G是星形圖,圈C或路P,f是恆等置換時;以及是任意置換時等 。