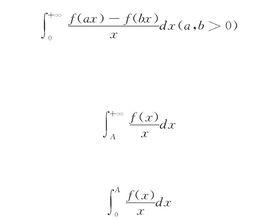基本介紹
傅汝蘭尼積分是一種特殊的含參變數的廣義積分，形如
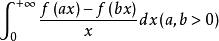傅汝蘭尼積分的廣義積分，其中f在(0，+∞)上連續。可精確計算的情形有 ：
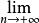傅汝蘭尼積分1.當f(0+)∈R， f(x)=f(+∞)∈R時，積分值為(f(0+)-f(+∞))ln(b/a)。
2.當f(0+)∈R，且存在A≥0，使
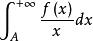傅汝蘭尼積分收斂時，積分值為f(0+)ln(b/a)；
3.當f(+∞)∈R，且存在A>0，使
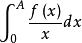傅汝蘭尼積分收斂時，積分值為f(+∞)ln(b/a) 。
傅汝蘭尼積分的證明
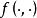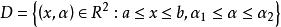傅汝蘭尼積分
傅汝蘭尼積分
傅汝蘭尼積分定理1 設 是定義在閉區間 的(二變數的)連續函式，讓 ，此時，下列性質成立 。
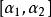傅汝蘭尼積分(i)F在 上連續。
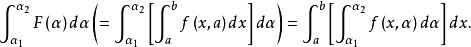傅汝蘭尼積分(ii)
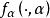傅汝蘭尼積分(iii)偏導函式 如在D連續，則F在[a，b]可微分而且
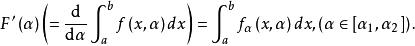傅汝蘭尼積分（以上定理的證明請參考相應文獻）
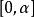傅汝蘭尼積分
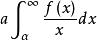傅汝蘭尼積分Frullani的積分 f是 上的連續函式，若對任意的 存在，則
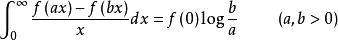傅汝蘭尼積分稱此為Frullani的積分 。
證明對任意α
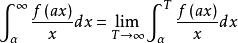傅汝蘭尼積分
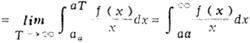傅汝蘭尼積分同理
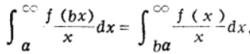傅汝蘭尼積分所以
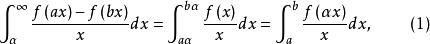傅汝蘭尼積分
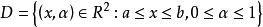傅汝蘭尼積分現令 ，在D的各點(x，α)研究與它對應的實數值f(αx)/x的函式，這個函式在閉區間D是連續的。因此，根據以上定理的(i)，由
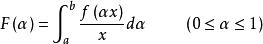傅汝蘭尼積分所定義的函式F在[0，1)連續。故
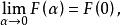傅汝蘭尼積分即
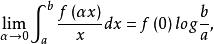傅汝蘭尼積分
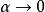傅汝蘭尼積分這樣， 時，(1)的左邊收斂，且
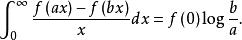傅汝蘭尼積分