基本介紹
 停時
停時 停時
停時 停時
停時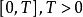 停時
停時停止時間是一種特殊的 隨機變數,表示一個隨機的時刻。例如,設為停時,那么這意味著兩方面內容,第一,是隨機的,第二,的取值範圍是為已知,當結果出現時,可表示為
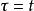 停時
停時也就是說,該隨機變數的結果是一個特定時刻。
現在考慮建立在債券上的美式期權,該期權可以在當前時刻t=0與到期日T之間的任何時刻執行,如果期權執行者認為時機已到,那么他將執行期權,否則他將選擇等待直到到期。
所以,我們需要研究一個“隨機日期”,它對於期權定價非常重要,實際上,提前執行的權力為美式期權增加了額外的價值。
 停時
停時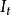 停時
停時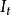 停時
停時我們設為期權的執行日期,很顯然已知信息集,我們就可以知道該期權是否已經被執行,也就是說,已知,我們可以知道哪種情況成立:
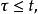 停時
停時該式表示期權已經被執行,或者
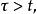 停時
停時該式表示期權尚未被提前執行。
 停時
停時的這種性質可以用來定義停止時間。
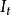 停時
停時定義1 停止時間是可測的非負隨機變數,滿足
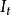 停時
停時1)已知,我們可以判斷是否有
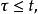 停時
停時2)我們有
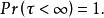 停時
停時 停時
停時對於一般的衍生證券,期限都是有限的,因此期權要么在一個有限的時刻被執行,要么過期失效,這意味著第二個等式,即以1機率有限,將恆成立。
停時的基本性質
下面列出停時的基本性質。
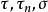 停時
停時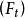 停時
停時定理 設均為停時,則有
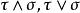 停時
停時(1)是停時;
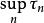 停時
停時(2)是停時;
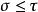 停時
停時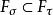 停時
停時(3)如果,則;
 停時
停時 停時
停時(4)是可測的。
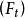 停時
停時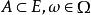 停時
停時首次進入某個集合或者首次達到的時刻是一個停時。事實上,設E是一個度量空間,X是關於濾子適應的、E為狀態空間的隨機過程,對於,定義
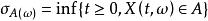 停時
停時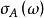 停時
停時則就是一個停時。
停時的作用
 停時
停時在實際操作中,我們應該如何利用停時呢?
 停時
停時最明顯的一個用途是用來代表期權的執行時間,對歐式期權而言,執行時間不含隨機因素,期權只能在到期日被執行,因而我們有
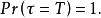 停時
停時 停時
停時而對於美式期權,一般是隨機的。
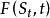 停時
停時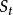 停時
停時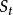 停時
停時考慮一份美式看漲期權,標的資產為,滿足以下SDE:
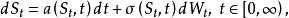 停時
停時其中漂移項和擴散項係數滿足一般的規範性條件。
和過去一樣,衍生證券的價格可以在等價鞅測度Q下表示,但此時多了一個複雜之處,證券持有者不一定要等到T時刻才執行期權,他可以在利潤較高時提前執行。
也就是說,如果持有者必須等到到期日才能執行期權,那么該期權 t 時刻價值為
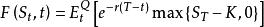 停時
停時而如果他可以提前執行,那么價值為
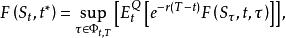 停時
停時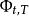 停時
停時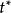 停時
停時 停時
停時 停時
停時其中是所有可能停止機會的集合,是的最優選擇,這裡代表期權持有者可能執行該看漲期權的日期。
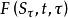 停時
停時 停時
停時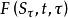 停時
停時因此在 t 時刻,我們可以計算出一系列,包含所有停止時間可能的取值,為了求出正確的價格,我們要求這些的上確界。

