概念
信息增益(Kullback–Leibler divergence)又稱information divergence,information gain,relative entropy 或者KLIC。
在機率論和資訊理論中,信息增益是非對稱的,用以度量兩種機率分布P和Q的差異。信息增益描述了當使用Q進行編碼時,再使用P進行編碼的差異。通常P代表樣本或觀察值的分布,也有可能是精確計算的理論分布。Q代表一種理論,模型,描述或者對P的近似。
儘管信息增益通常被直觀地作為是一種度量或距離,但事實上信息增益並不是。就比如信息增益不是對稱的,從P到Q的信息增益通常不等於從Q到P的信息增益。信息增益是f增益(f-divergences)的一種特殊情況。在1951年由Solomon Kullback 和Richard Leibler首先提出作為兩個分布的直接增益(directed divergence)。它與微積分中的增益不同,但可以從Bregman增益(Bregman divergence)推導得到。
定義
設離散隨機變數的機率分布 P和 Q,它們的信息增益定義為
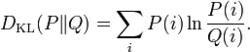 信息增益
信息增益其中分布 P和 Q必須是機率分布,而且對於任何P(i)>0,必須有Q(i)>0。當P(i)=0時,公式的值為0。從公式看,信息增益是以分布 P為權重的 P和 Q對數差值的加權平均。
信息增益的連續分布形式:
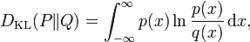 信息增益
信息增益其中 p和 q表示 P和 Q的密度機率函式
更一般地,P和Q是集合X上的機率測度,Q關於P絕對連續,從P到Q的信息增益定義為
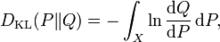 信息增益
信息增益假設右式存在,dQ/dp是Q關於P的Radon-Nikodym導數,
如果P關於Q也絕對連續,那么上式可變為
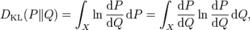 信息增益
信息增益上式可視為P關於Q的熵。如果u是集合X上的任何測度,即有p=dP/du和q=dQ/du存在,那么從P到Q的信息增益可定義為
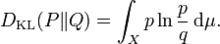 信息增益
信息增益當信息以比特為單位時,公式中的對數的基數為2。當信息以nats為單位時,基數為e。大多數包括信息增益公式的公式都使對數函式保持原樣,即與基數無關。
注意,信息增益是要講方向的,上述公式都是計算從P到Q的信息增益。
特徵選擇
在信息增益中,衡量標準是看特徵能夠為分類系統帶來多少信息,帶來的信息越多,該特徵越重要。對一個特徵而言,系統有它和沒它時信息量將發生變化,而前後信息量的差值就是這個特徵給系統帶來的信息量。所謂信息量,就是熵。
假如有變數X,其可能的取值有n種,每一種取到的機率為Pi,那么X的熵就定義為
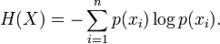 熵公式
熵公式也就是說X可能的變化越多,X所攜帶的信息量越大,熵也就越大。對於文本分類或聚類而言,就是說文檔屬於哪個類別的變化越多,類別的信息量就越大。所以特徵T給聚類C或分類C帶來的信息增益為IG(T)=H(C)-H(C|T)。
H(C|T)包含兩種情況:一種是特徵T出現,標記為t,一種是特徵T不出現,標記為t'。所以
H(C|T)=P(t)H(C|t)+P(t')H(C|t‘),再由熵的計算公式便可推得特徵與類別的信息增益公式。
信息增益最大的問題在於它只能考察特徵對整個系統的貢獻,而不能具體到某個類別上,這就使得它只適合用來做所謂“全局”的特徵選擇(指所有的類都使用相同的特徵集合),而無法做“本地”的特徵選擇(每個類別有自己的特徵集合,因為有的詞,對這個類別很有區分度,對另一個類別則無足輕重)。
方法
包括直方圖相交(historgram intersection),開方統計(Chi-square statistic),quadratic form distance,賽程(match distance),Kolomogorov-Smirnov distance和earth mover's distance

