設{f}(x)}是定義在可測集E上幾乎處處有限的可測函式列,f(x)是E上幾乎處處有限的可測函式,若對任給。}0,
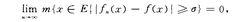 依測度收斂
依測度收斂則{f}(x)}稱為依測度收斂於f (x).這個概念經過推廣,在機率論中也有用.
依測度收斂(convergence in measure)是實變函式論中重要的收斂概念之一。
設{f}(x)}是定義在可測集E上幾乎處處有限的可測函式列,f(x)是E上幾乎處處有限的可測函式,若對任給。}0,
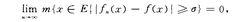 依測度收斂
依測度收斂則{f}(x)}稱為依測度收斂於f (x).這個概念經過推廣,在機率論中也有用.
ε , μ
依機率收斂,convergence in probability,別稱隨機收斂,套用於機率論與數理統計。
依機率收斂 定義 性質 參見強收斂是指測度網(或列)依範數(能量)的收斂。關於點列的收斂性包括兩種:強收斂和弱收斂,並且它們之間存在著這樣的關係:強收斂必定弱收斂,但弱收斂不一定強收斂。
定義 X與其共軛空間中運算元列的收斂性 X與Y空間中運算元列的收斂性本書論述測度論和以測度為基礎的機率論的基本知識和方法,包括集及其勢、距離空間、測度與機率、可測函式與隨機變數、積分與數學期望、乘積測度與獨立、Radon...
內容簡介 目錄幾乎處處收斂是處處收斂概念的推廣。設 X 是隨機變數,Xn是隨機變數序列,如果P(Xn→X)=1(n→∞),則稱Xn幾乎處處收斂於X。
定義 收斂比較定理《測度與機率》是由 嚴士健,劉秀芳編著的,北京師範大學出版社出版。本書的特點是讀者不必學習實變函式論而學習測度論;測度論與機率論的基本內容緊密結合而更有...
測度與機率 內容簡介 目錄機率論中的極限定理和數理統計學中各種統計量的極限性質,都是按隨機變數序列的各種不同的收斂性來研究的。
《測度與積分原理 》,由西安電子科技大學出版社出版。描述的是本書在比較完整、系統地介紹Lebesgue測度、Lebesgue積分理論的前提下,穿插介紹了...
基本信息 內容簡介 編輯推薦 目錄《測度與積分》是2002年西安電子科技大學出版社出版的一本書籍。
基本信息 內容介紹 目錄