求解方程時的余函式
基本介紹
對於非齊次線性微分方程(L):
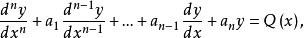 余函式
余函式考慮令右邊為0的齊次線性微分方程(H)
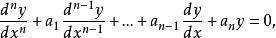 余函式
余函式(L)的通解由(H)的通解與(L)的一個特解之和給出。因而把(H)的通解稱為(L)的余函式。
n階齊次常係數線性微分方程的余函式
齊次常係數線性微分方程解法的一個主要特點是,不用積分僅用代數方法就能求出方程的通解,即 余函式。
n階齊次常係數線性微分方程
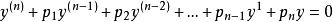 余函式
余函式的特徵方程為
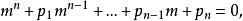 余函式
余函式同樣,該代數方程的根決定了 n階齊次常係數線性微分方程通解的形式。
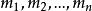 余函式
余函式①具有n個相異的根,則其餘函式為
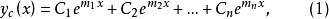 余函式
余函式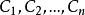 余函式
余函式式中,為n個任意常數。
 余函式
余函式②特徵方程有一對單復根,則其餘函式為
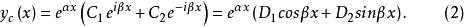 余函式
余函式③特徵方程有k重實根m,則其餘函式有k項,為
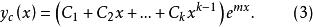 余函式
余函式④若特徵方程有一對k重複根,則其餘函式有2k項,為
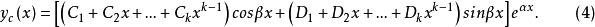 余函式
余函式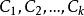 余函式
余函式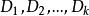 余函式
余函式在式(2)~式(4)中,和分別為k個任意常數。
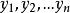 余函式
余函式總之,解n階齊次常係數線性微分方程通解可以不用積分,只要求出齊次線性微分方程特徵方程n個線性無關的根,則有微分方程的通解式
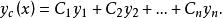 余函式
余函式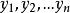 余函式
余函式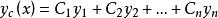 余函式
余函式若線性相關,則不是n階齊次常係數線性微分方程的通解。
三角函式的余函式
定義
設f與g為兩個三角函式,α為任意角,β為它的餘角。如果f在α所取的值等於g在β所取的值,則稱f與g互為余函式。例如正弦與餘弦,正切與餘切等。
詳細分析
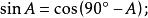 余函式
余函式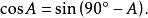 余函式
余函式由上面兩個公式(一個角的正弦等於它的餘角的餘弦,一個角的餘弦等於它的餘角的正弦)可知正弦與餘弦互相稱為余函式。
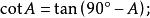 余函式
余函式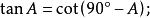 余函式
余函式由上面兩個公式(一個角的正切等於它的餘角的餘切)可知正切與餘切互相稱為余函式。
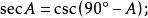 余函式
余函式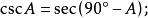 余函式
余函式由上面兩個公式(一個角的正割等於它的餘角的餘割)可知正割與餘割互相稱為余函式。

