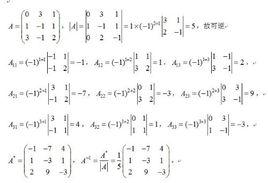定義
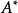 伴隨矩陣
伴隨矩陣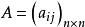 伴隨矩陣
伴隨矩陣 伴隨矩陣
伴隨矩陣 伴隨矩陣
伴隨矩陣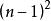 伴隨矩陣
伴隨矩陣 伴隨矩陣
伴隨矩陣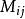 伴隨矩陣
伴隨矩陣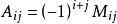 伴隨矩陣
伴隨矩陣 伴隨矩陣
伴隨矩陣設矩陣 ,將矩陣 的元素 所在的第i行第j列元素划去後,剩餘的 ,各元素按原來的排列順序組成的n-1階矩陣所確定的行列式稱為元素 的餘子式,記為 ,稱 謂元素 的代數餘子式。
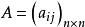 伴隨矩陣
伴隨矩陣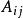 伴隨矩陣
伴隨矩陣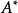 伴隨矩陣
伴隨矩陣方陣 的各元素的代數餘子式 所構成的如下矩陣 :
 伴隨矩陣
伴隨矩陣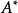 伴隨矩陣
伴隨矩陣 伴隨矩陣
伴隨矩陣該矩陣 稱為矩陣 的伴隨矩陣 。
性質
伴隨矩陣是矩陣理論及線性代數中的一個基本概念,是許多數學分支研究的重要工具,伴隨矩陣的一些新的性質被不斷發現與研究。伴隨矩陣的一些基本性質如下 :
 伴隨矩陣
伴隨矩陣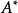 伴隨矩陣
伴隨矩陣(1) 可逆若且唯若 可逆;
 伴隨矩陣
伴隨矩陣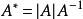 伴隨矩陣
伴隨矩陣(2)如果 可逆,則 ;
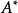 伴隨矩陣
伴隨矩陣(3)對於 的秩有:
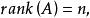 伴隨矩陣
伴隨矩陣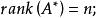 伴隨矩陣
伴隨矩陣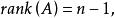 伴隨矩陣
伴隨矩陣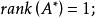 伴隨矩陣
伴隨矩陣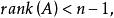 伴隨矩陣
伴隨矩陣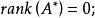 伴隨矩陣
伴隨矩陣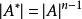 伴隨矩陣
伴隨矩陣(4) ;
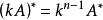 伴隨矩陣
伴隨矩陣(5) ;
 伴隨矩陣
伴隨矩陣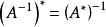 伴隨矩陣
伴隨矩陣(6)若 可逆,則 ;
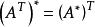 伴隨矩陣
伴隨矩陣(7) ;
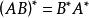 伴隨矩陣
伴隨矩陣(8) 。
特殊求法
(1)當矩陣是大於等於二階時 :
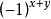 伴隨矩陣
伴隨矩陣 伴隨矩陣
伴隨矩陣 伴隨矩陣
伴隨矩陣 伴隨矩陣
伴隨矩陣 伴隨矩陣
伴隨矩陣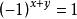 伴隨矩陣
伴隨矩陣主對角元素是將原矩陣該元素所在行列去掉再求行列式,非主對角元素是原矩陣該元素的共軛位置的元素去掉所在行列求行列式乘以 , , 為該元素的共軛位置的元素的行和列的序號,序號從1開始。主對角元素實際上是非主對角元素的特殊情況,因為 = ,所以,一直是正數,沒必要考慮主對角元素的符號問題。
(2)當矩陣的階數等於一階時,伴隨矩陣為一階單位方陣。
(3)二階矩陣的求法口訣:主對角線元素互換,副對角線元素加負號 。
m重伴隨矩陣
 伴隨矩陣
伴隨矩陣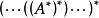 伴隨矩陣
伴隨矩陣 伴隨矩陣
伴隨矩陣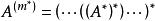 伴隨矩陣
伴隨矩陣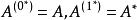 伴隨矩陣
伴隨矩陣設 為n階方陣,則稱n階方陣 為 的m重伴隨矩陣 ,記為:,其中括弧為m重。特別地, 。