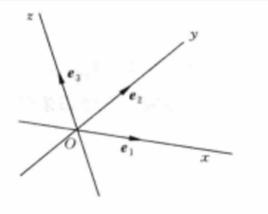
坐標系
坐標法的基礎是建立坐標系,坐標系的實質是平面或空間的點到有序數組的對應關係。為此首先要建立一個參考系,即坐標標架。
例如,平面上由兩條互相垂直並且都以交點為零點的兩條數軸構成一個平面直角標架,產生一個平面直角坐標系;在平面上取定一條射線,就得到一個平面的極坐標系.這兩種坐標系都是用距離、夾角等度量概念來規定坐標的。現在我們用向量的分解度量建立一種新的坐標系,即仿射坐標系。它不涉及度量概念,從而更加適用於仿射幾何學。
仿射坐標系
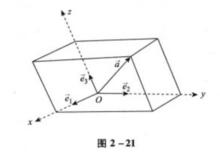 圖1
圖1 仿射坐標系
仿射坐標系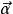 仿射坐標系
仿射坐標系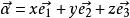 仿射坐標系
仿射坐標系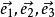 仿射坐標系
仿射坐標系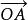 仿射坐標系
仿射坐標系假設是不共面的向量(圖1),則根據分解定理,對任一向量存在唯一實數組x,y,z,使得。這樣,就得到從全體向量的集合到全體三元有序數組的集合的一個一一對應關係。即一方面不同的向量對向量組有不同的分解係數,另一方面每個三元有序數組一定是某個向量的分解係數。取定空間中的一點O,則又有從空間到全體向量的集合的一一對應關係:點A對應到向量。
把上述兩個一一對應關係結合起來,就得到從空間到全體三元有序數組集合的一一對應關係,這就產生了仿射坐標系。
定義
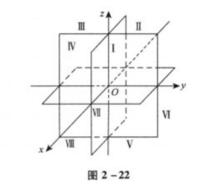 圖2
圖2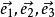 仿射坐標系
仿射坐標系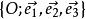 仿射坐標系
仿射坐標系空間中的一個定點O連同不共面的3個有序向量的全體叫做空間的一個仿射標架,記作:。
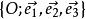 仿射坐標系
仿射坐標系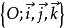 仿射坐標系
仿射坐標系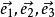 仿射坐標系
仿射坐標系當標架中3向量為單位向量時,稱為笛卡爾標架;當笛卡爾標架中的3單位向量互相垂直時,稱為直角標架,記作:。稱O為它的原點,稱為它的坐標向量。
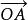 仿射坐標系
仿射坐標系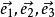 仿射坐標系
仿射坐標系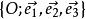 仿射坐標系
仿射坐標系對於空間的任意一點A,把向量對的分解係數構成的有序數組稱為點A關於上述仿射標架的仿射坐標。這樣得到的空間的點與三元有序數組(x,y,z)的對應關係稱為由仿射標架決定的空間仿射坐標系。
 表1
表1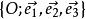 仿射坐標系
仿射坐標系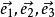 仿射坐標系
仿射坐標系取定仿射標架後,把經過原點O,平行於坐標向量並且以其方向為正方形的數軸稱為坐標軸。3條坐標軸分別為x軸、y軸和z軸,它們分別平行於;兩條坐標軸決定的平面稱為坐標平面,如x軸和y軸決定的平面叫做xoy平面等。三張坐標平面將空間分割成8塊,稱為8個卦限。
空間直角坐標系如圖2所示,空間點的坐標在各卦限的符號見表1。
向量的坐標
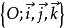 仿射坐標系
仿射坐標系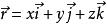 仿射坐標系
仿射坐標系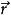 仿射坐標系
仿射坐標系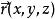 仿射坐標系
仿射坐標系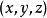 仿射坐標系
仿射坐標系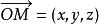 仿射坐標系
仿射坐標系在標架中,若,稱x,y,z為向量的坐標,記作或。特別地,點M(x,y,z)對於原點O的向徑。
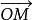 仿射坐標系
仿射坐標系位置向量:在標架下,以原點O為起點,M為終點的向量稱為M的向徑,或稱為位置向量,記作。
坐標軸上點的坐標的特點:有兩個坐標為零。
坐標平面上點的坐標的特點:有一個坐標為零。坐標原點的三個坐標都為零。
向量坐標運算
1、向量的坐標
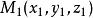 仿射坐標系
仿射坐標系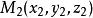 仿射坐標系
仿射坐標系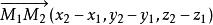 仿射坐標系
仿射坐標系起點為,終點為的向量的坐標是,終點坐標減去起點的同名坐標。
2、向量的坐標運算
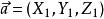 仿射坐標系
仿射坐標系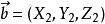 仿射坐標系
仿射坐標系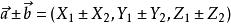 仿射坐標系
仿射坐標系設,,則,同名坐標相加(減)。
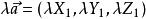 仿射坐標系
仿射坐標系,用數去乘每個分量。