奇異積分的交換子

奇異積分的交換子

正文

調和分析中典型的一類非卷積運算元。設T1,T2是兩個運算元（一般說來，設它們的作用次序是不可交換的，即T1T2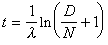T2T1），定義T1與T2的交換子為T1T2－T2T1，記為【T1,T2】，即

【T1,T2】＝T1T2-T2T1。

如果在L2(R)中取T1＝A為用函式A(x)作乘法的運算元，即A(ƒ)(x)＝A(x)ƒ(x),取T2為奇異積分即希爾伯特變換H或它與微分運算元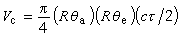的整數次冪的乘積,這時所得到的交換子稱為奇異積分的交換子。例如,C1(ƒ)=【A,DH】ƒ就是一個奇異積分的交換子。形式地在積分號下取微商，得到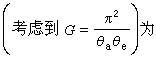

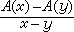注意到H是 L2有界的，容易猜測：只要A┡(x)∈L∞，即本性有界,C1(ƒ)對ƒ來說是L2到L2有界的。但由於這個運算元不是卷積運算元，這個猜測較難驗證。直到1965年才被A.P.考爾德倫用複雜的複分析技巧加以證明。對DnH,與A作n次的交換子運算,便得到高階奇異積分的交換子（省略一個常數因子）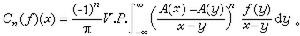

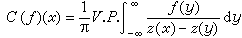
考爾德倫的方法不適用於高階的情形。1975年R.考伊夫曼與Y.邁耶用實分析的方法證明了：若A┡(x)∈L∞，則Cn(ƒ)是L2到L2的有界運算元。1982年他們與A.麥金托什合作,通過對Cn(ƒ)的運算元模作精確的估計,證實了關於李普希茨曲線上柯西積分運算元的考爾德倫猜想:若A┡∈L∞，則定義在複平面的李普希茨曲線z(x)＝x+iA(x)上的柯西積分運算元

是L2到L2有界的。
奇異積分交換子的研究,與BMO（有界平均振動）函式有密切聯繫（見BMO 空間）。例如，1976年R.R.科伊夫曼、R.羅奇伯格與G.韋斯證明了，最簡單的奇異積分的交換子

對ƒ來說是L2到L2有界的充分必要條件是A為BMO函式,並且交換子的運算元模與A的BMO模的大小是差不多的。
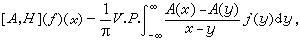
奇異積分交換子的結果與方法，在調和分析、偏微分方程與非線性分析中有著愈來愈廣泛的套用。由於它不是卷積運算元，因此，許多古典調和分析的技巧不能直接套用，需要尋求新的方法。
參考書目
　A.P.Calderón, Commutators of Singular IntegralOperators,Proc. nat. Acad. Sci. U. S. A.,53, pp.1092～1099,1965.
　A.P.Calderón,Commutators,Singular Integral on Lipschitz Curves and Applications,Proc.of the I. C. M.,Helsinki, 1978.
　Y.Meyer,Intégrales Singulières, Opérateurs Multilinéaires,Analyse Complexe et Equations aux Derivées Partielles,Proc.of the I.C.M.,Warszawa,1983.

配圖

相關連線