概念
量子場論中,微觀因果性與么正性、譜條件、交叉對稱性等原理結合起來,也可以導出散射振幅滿足的色散關係。
用色散關係研究強作用時,是將解析性與么正性、譜條件、交叉對稱性等相結合,使得到的許多物理過程的散射振幅相互聯繫,得出一組耦合的方程式。利用它們可以對強作用進行唯象分析。
基本原理
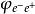 交叉對稱性
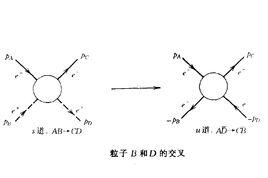
交叉對稱性為得到,還可以簡單地運用反粒子描述,見圖1“交叉”的結果,按這種方式,有:
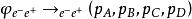 交叉對稱性
交叉對稱性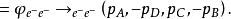 交叉對稱性
交叉對稱性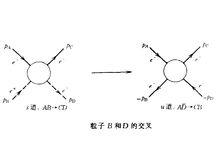 圖1
圖1 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性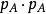 交叉對稱性
交叉對稱性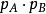 交叉對稱性
交叉對稱性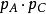 交叉對稱性
交叉對稱性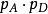 交叉對稱性
交叉對稱性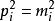 交叉對稱性
交叉對稱性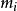 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性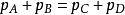 交叉對稱性
交叉對稱性考慮過程,它有兩個獨立的運動學變數,例如入射能量和散射角。通常需要把表示成為Lorentz變換下的不變數的函式,這些不變數是粒子的四動量的標量積,,,等,由於(是第個粒子的靜止質量)和能量-動量守恆,不變數中只有兩個是獨立的。習慣上往往採用Mandelstam變數:
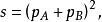 交叉對稱性
交叉對稱性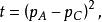 交叉對稱性
交叉對稱性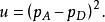 交叉對稱性
交叉對稱性它們滿足如下關係式:
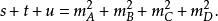 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性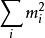 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性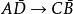 交叉對稱性
交叉對稱性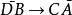 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性為表現由交叉相聯繫的過程的運動學或物理的區域,構造一個保持,,對稱的二維圖。畫出三個軸,,,使之構成高為的等邊三角形(圖2)。從三角形內或外(注意,,的符號)任一點到三軸垂直距離之和等於三角形的高度。是過程的質心繫總能量的平方,習慣上稱為道過程。在前一例中,道反應為,交叉反應和分別稱為道和道,因為和分別等於該道的質心繫能量。對不等質量粒子的散射,物理區域的邊界更複雜,但存在三個不相交區域這個一般性結論仍然成立。
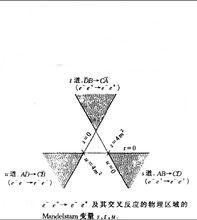 圖2
圖2 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性將作為道過程,容易證明:
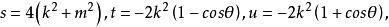 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性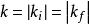 交叉對稱性
交叉對稱性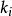 交叉對稱性
交叉對稱性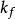 交叉對稱性
交叉對稱性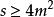 交叉對稱性
交叉對稱性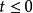 交叉對稱性
交叉對稱性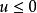 交叉對稱性
交叉對稱性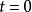 交叉對稱性
交叉對稱性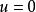 交叉對稱性
交叉對稱性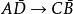 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性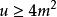 交叉對稱性
交叉對稱性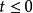 交叉對稱性
交叉對稱性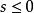 交叉對稱性
交叉對稱性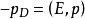 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性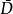 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性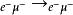 交叉對稱性
交叉對稱性其中是質心繫散射角,,和分別為入射和散射電子在質心繫中的動量。還可以證明這一過程只有當,,時才是物理上允許的。這一物理區域在圖2中用陰影標出。注意,()對應於向前(向後)散射。對於交叉反應(),變成質心繫總能量的平方,這一過程在不同運動學區域才能實現:,,。需要注意,而,為入射的能量。如果道過程為,該反應和交叉反應的物理區域的邊界由下式給出:
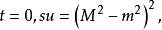 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性 交叉對稱性
交叉對稱性其中和分別為電子和子的質量。利用無自旋電子-正電子散射不變幅式子和交叉關係式子的形式,可以推導出:
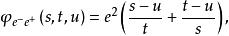 交叉對稱性
交叉對稱性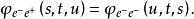 交叉對稱性
交叉對稱性採用Mandelstam變數,可寫為:
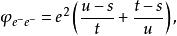 交叉對稱性
交叉對稱性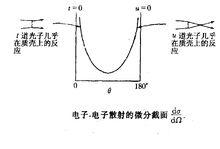 圖3
圖3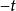 交叉對稱性
交叉對稱性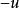 交叉對稱性
交叉對稱性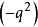 交叉對稱性
交叉對稱性由此計算的截面畫在圖3上,明顯給出向前和向後的峰。和分別是動量轉移的平方,即虛光子動量的平方。當光子的動量平方很小時,即它幾乎在質殼上,由不確定性原理,相互作用的力程非常大,因此相應的截面非常大。