二體問題

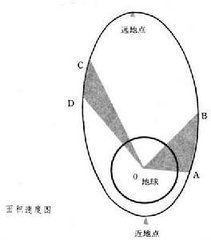
二體問題的解是研究行星繞太陽，太空飛行器繞中心天體運動的近似解，是進一步研究更複雜的天體運動的基礎。在二體問題中，只要知道兩個天體在初始時刻的位置和速度，就可以計算出兩天體在任意時刻的位置和速度。

二體問題

正文

研究兩個質點在萬有引力作用下的運動規律。二體問題是天體力學中的一個基本問題。J.克卜勒仔細分析了丹麥天文學家第谷·布拉赫多年的觀測資料，在研究火星繞太陽運動的基礎上總結出描述行星運動的三大定律。I.牛頓隨後提出的萬有引力揭示了產生這些運動現象的原因。從萬有引力和牛頓第二定律出發，用數學方法可以嚴格證明克卜勒三大定律，於是二體問題得到徹底解決。太空飛行器受到中心天體的吸引力，把這個引力看成質點引力時，太空飛行器圍繞中心的運動問題就是二體問題。由於太空飛行器質量遠比中心體質量小，人們將這種問題稱為限制性二體問題。太空飛行器的運動情況也可近似地用克卜勒定律來描述：①太空飛行器運動始終在一個平面內，這個平面稱為軌道平面，中心體的質心在這個平面內。根據太空飛行器軌道速度大小和方向不同，太空飛行器圍繞中心體質心的軌道可以是圓、橢圓、拋物線或雙曲線。中心體質心位於這些曲線的一個焦點上，這些軌道統稱克卜勒軌道。②太空飛行器與中心體質心的連線在相同的時間裡掃過的面積相同。它反映太空飛行器在軌道上各點運動速度之間的比例關係，離中心體越遠太空飛行器速度就越小。③太空飛行器在橢圓軌道上運行時，運行周期的平方與軌道半長軸的立方成正比。它給出運行一周的時間與軌道大小的關係。在二體問題中，只要知道兩個天體在初始時刻的位置和速度，就可以計算出兩天體在任意時刻的位置和速度。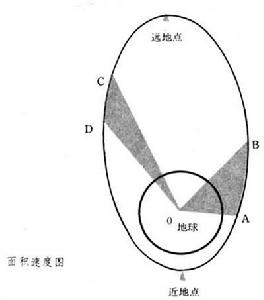

二體問題

配圖

相關連線